题目内容
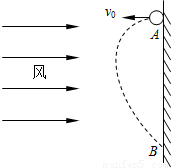
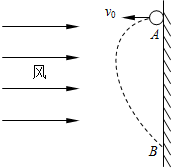如图所示，在足够高的竖直墙面上A点，以水平速度v0向左抛出一个质量为m的小球，小球抛出后始终受到水平向右的恒定风力的作用，风力大小为F，经过一段时间小球将再次到达墙面上的B点处，重力加速度为g，则在此过程中：（1）小球在水平方向和竖直方向各作何种运动？
（2）小球水平方向的速度为零时距墙面的距离？
（3）墙面上A、B两点间的距离？
（4）小球的最大速率vmax？
（5）小球的最小速率vmin？
分析：（1）将小球的运动分解为水平方向和竖直方向，在水平方向上受到恒力作用，先向左做匀减速运动，然后向右做匀加速运动；在竖直方向上仅受重力，做自由落体运动．
（2）根据水平方向上的运动规律，结合速度位移公式和牛顿第二定律求出小球水平方向的速度为零时距墙面的距离．
（3）根据水平方向上向左和向右运动的对称性，求出运动的时间，抓住等时性求出竖直方向A、B两点间的距离．
（4）小球到达B点时水平方向的速度最大，竖直方向上的速度最大．则B点的速度最大，根据运动学公式，结合平行四边形定则求出最大的速度大小．
（5）将小球的速度方向沿合力方向和垂直于合力方向分解，垂直于合力方向做匀速直线运动，当沿合力方向的速度为零时，小球的速度最小，根据平行四边形定则，结合几何关系求出最小速率．
（2）根据水平方向上的运动规律，结合速度位移公式和牛顿第二定律求出小球水平方向的速度为零时距墙面的距离．
（3）根据水平方向上向左和向右运动的对称性，求出运动的时间，抓住等时性求出竖直方向A、B两点间的距离．
（4）小球到达B点时水平方向的速度最大，竖直方向上的速度最大．则B点的速度最大，根据运动学公式，结合平行四边形定则求出最大的速度大小．
（5）将小球的速度方向沿合力方向和垂直于合力方向分解，垂直于合力方向做匀速直线运动，当沿合力方向的速度为零时，小球的速度最小，根据平行四边形定则，结合几何关系求出最小速率．
解答：解：（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）将小球的运动沿水平方向和竖直方向分解
水平方向：F=max，得ax=
则x=
=
．
（3）水平方向速度减小为零所需的时间t1=
所以t=2t1=
=
．
竖直方向上：y=
gt2=
．
（4）小球运动到B点的速度最大．
vx=v0
vy=gt=
vmax=
=
．
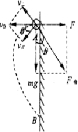
（5）将运动沿图示方向分解．
当v⊥=0时，小球速度最小．
此时vmin=v∥=v0cosθ
根据力的关系知cosθ=
．
解得vmin=
．
答：（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）小球水平方向的速度为零时距墙面的距离为
．
（3）墙面上A、B两点间的距离为
．
（4）小球的最大速率为vmax=
．
（5）小球的最小速率为vmin=
．
（2）将小球的运动沿水平方向和竖直方向分解
水平方向：F=max，得ax=
| F |
| m |
则x=
| v02 |
| 2ax |
| mv02 |
| 2F |
（3）水平方向速度减小为零所需的时间t1=
| v0 |
| ax |
所以t=2t1=
| 2v0 |
| ax |
| 2mv0 |
| F |
竖直方向上：y=
| 1 |
| 2 |
| 2m2gv02 |
| F2 |
（4）小球运动到B点的速度最大．
vx=v0
vy=gt=
| 2mgv0 |
| F |
vmax=
| vx2+vy2 |
| v0 |
| F |
| F2+4m2g2 |
（5）将运动沿图示方向分解．
当v⊥=0时，小球速度最小．
此时vmin=v∥=v0cosθ
根据力的关系知cosθ=
| mg | ||
|
解得vmin=
| mgv0 | ||
|
答：（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）小球水平方向的速度为零时距墙面的距离为
| mv02 |
| 2F |
（3）墙面上A、B两点间的距离为
| 2m2gv02 |
| F2 |
（4）小球的最大速率为vmax=
| v0 |
| F |
| F2+4m2g2 |
（5）小球的最小速率为vmin=
| mgv0 | ||
|
点评：解决本题的关键将小球的运动分解，搞清在分运动的规律，结合等时性，运用牛顿第二定律和运动学公式进行求解．
练习册系列答案
阅读快车系列答案
相关题目
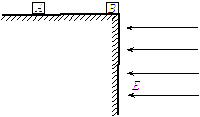
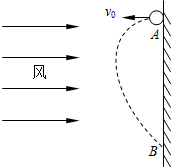如图所示，在足够高的竖直墙面上A点，以水平速度v0向左抛出一个质量为m的小球，小球抛出后始终受到水平向右的恒定风力的作用，风力大小为F，经过一段时间小球将再次到达墙面上的B点处，重力加速度为g，则在此过程中：
