题目内容
20. 如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求:
如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求:(1)B、A两点的电势差UBA;
(2)电场强度E;
(3)小球到达B点时,悬线对小球作用力.
分析 (1)小球从A到B的过程中,重力做正功mglsin60°,电场力做功为-qUBA,动能的变化量为零,根据动能定理求解电势差UBA.
(2)根据电场强度与电势差的关系U=Ed求解场强E.式中d是AB沿电场线方向的距离.
(3)小球到达B点时,速度为零,向心力为零,根据牛顿第二定律求解拉力.
解答 解:(1)根据动能定理:
mglsin60°-qUBA=0-0
B、A两点的电势差:
UBA=$\frac{mglsin60°}{q}$=$\frac{\sqrt{3}mgl}{2q}$
(2)电场强度:
E=$\frac{{U}_{BA}}{d}$=$\frac{\sqrt{3}mgl}{2ql(1-cos60°)}$=$\frac{\sqrt{3}mq}{q}$
(3)小球到达B点时,悬线对小球的拉力T、重力沿半径方向的分力mgcos30°、电场力沿半径方向的分力qEcos60°的合力是向心力: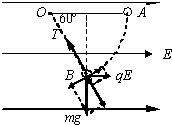
因为vB=0,故:
T-mgcos30°-qEcos60°=0
解得:
T=$\sqrt{3}$mg
答:(1)B、A两点的电势差UBA为$\frac{\sqrt{3}mgl}{2q}$;
(2)电场强度E为$\frac{\sqrt{3}mq}{q}$;
(3)小球到达B点时,悬线对小球作用力为$\sqrt{3}$mg.
点评 解决本题关键要掌握动能定理和电场力做功W=qU、电场强度与电势差的关系式U=Ed.注意在平衡位置是速度最大,不为零.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
11. 如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心0,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的勻强电场中.将小环从 A点由静止释放,小环运动到B点时速度恰好为O.已知小环在A、B两点时弹簧的形变量大小相等.则( )
如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心0,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的勻强电场中.将小环从 A点由静止释放,小环运动到B点时速度恰好为O.已知小环在A、B两点时弹簧的形变量大小相等.则( )
 如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心0,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的勻强电场中.将小环从 A点由静止释放,小环运动到B点时速度恰好为O.已知小环在A、B两点时弹簧的形变量大小相等.则( )
如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心0,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的勻强电场中.将小环从 A点由静止释放,小环运动到B点时速度恰好为O.已知小环在A、B两点时弹簧的形变量大小相等.则( )| A. | 小环从A点运动到B点的过程中,小环的电势能一直增大 | |
| B. | 小环从A点运动到B点的过程中,弹簧的弹性势能一直先增大后减小 | |
| C. | 电场强度的大小E=$\frac{mg}{q}$ | |
| D. | 小环在A点时受到大环对它的弹力大小F=mg+$\frac{1}{2}$kL |
8. 如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
 如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )| A. | 电源的输出功率为4W | B. | 电源的输出功率为2W | ||
| C. | 电源效率为33.3% | D. | 电源效率为66.7% |
15.下列说法正确的是( )
| A. | 作曲线运动的物体,位移的大小总小于路程 | |
| B. | 物体的位移就是物体运动轨迹的长度 | |
| C. | 在一直线上运动的物体,路程就等于位移的大小 | |
| D. | 物体的路程是矢量,而位移是标量 |
9.酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间.表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车制动时的加速度大小都相同).
分析表,求解下列问题
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
| 速度(m/s) | 思考距离/m | 制动距离/m | ||
| 正常 | 酒后 | 正常 | 酒后 | |
| 15 | 7.5 | 15.0 | 22.5 | 30.0 |
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
10.一个小铁球和一根羽毛同时从同一高处下落总是铁球先落地,这是因为( )
| A. | 铁球比羽毛重 | B. | 铁球比羽毛密度大 | ||
| C. | 羽毛受到的空气阻力相对大 | D. | 羽毛重力加速度小 |
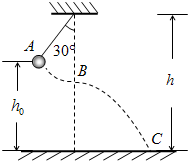 如图所示,让小球从图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断,设摆线长l=1.6m,悬点到地面的高度为h=6.6m,不计空气阻力,求摆球落地时的速度.
如图所示,让小球从图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断,设摆线长l=1.6m,悬点到地面的高度为h=6.6m,不计空气阻力,求摆球落地时的速度.