Question

【题目】碰撞一般分为弹性碰撞和非弹性碰撞,发生弹性碰撞时,系统的动量守恒、机械能也守恒;发生非弹性碰撞时,系统的动量守恒,但机械能不守恒.为了判断碰撞的种类,某实验兴趣小组设计了如下实验.

实验步骤如下:

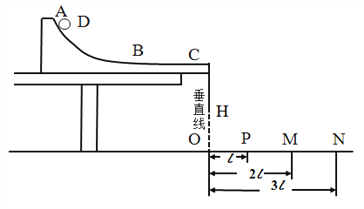
①按照如图所示的实验装置图,安装实物图;

②用石蜡打磨轨道,使ABC段平整光滑,其中AB段是曲面,BC段水平面,C端固定一重垂线;

③O是C点的竖直投影点,OC=H,在轨道上固定一挡板D,从贴紧挡板D处由静止释放质量为m1小球1,小球1落在M点,用刻度尺测得M点与O点距离2l;

④在C的末端放置一个大小与小球1相同的小球2,其质量为m2.现仍从D处静止释放小球1,小球1与小球2发生正碰,小球2落在N点,小球1落在P点,测得OP为l,ON为3l

(1)小球1与小球2的质量之比m1:m2=________;

(2)若两小球均看作质点,以两球为系统,碰前系统初动能Ek0________。碰后系统末动能Ek______,则系统机械能___________(填“守恒”“不守恒”),可以得出两球的碰撞是_________碰撞.Ek0、Ek用题目中字母H、m2、和重力加速度g表示)

Answer 1

【答案】 （1）3：1 （2） 守恒 弹性

【解析】（i）球1运动到C端的速度为v1，在空中做平抛运动．
水平方向：2l=v1t，竖直方向：H=gt2，
解得：v1=2l
由于球1两次均从同一高度自由下滑，到C端动能一样，速度均为v1，设球1与球2碰撞后速度分别为：v1′、v2′，
解得：v1′=l；v2′=3l

碰撞前后系统动量守恒，以向右为正方向，以球1和球2为系统，由动量守恒定律得：m1v1=m1v1′+m2v2′，
碰后两均在空中做平抛运动：
球1水平方向：l=v1′t，
球2水平方向：3l=v2′t，
则有：m1×2l=m1×l+m2×3l
解得： ；
（ ii）以两球为系统，碰前系统初动能：EK0=m1v12=
碰后系统末动能：EK=m1v1′2+m2v2′2=
把质量与速度代入整理得：EK0=EK，则碰撞过程系统机械能守恒，两球碰撞是弹性碰撞；