题目内容
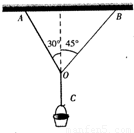
在水平天花板下，两根轻绳共同悬挂一吊篮．已知AO绳与竖直方向成30°角，BO绳与 竖直方向夹角为45°，若AO绳和CO绳能承受的拉力足够大，若BO绳能承受的最大拉力为100N，求吊篮和其中的物体总质量不应超过多少千克？（结果保留一位小数）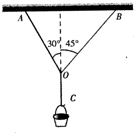
以O点为原点建立直角坐标系，
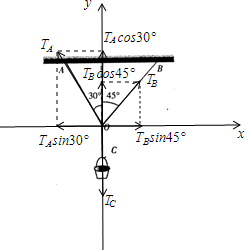
根据平衡条件有：F合=0
沿x轴：TAsin30°=TBsin45°
TB最大取100N，所以TBsin45°=50
N
解得：TA=100
N
沿y轴：TAcos30°+TBcos45°=TC
解得：TC=193.1N
又吊篮处于平衡状态：
故：TC=mCg
所以mC=19.3kg
答：吊篮和其中的物体总质量不应超过19.3千克．
根据平衡条件有：F合=0
沿x轴：TAsin30°=TBsin45°
TB最大取100N，所以TBsin45°=50
| 2 |
解得：TA=100
| 2 |
沿y轴：TAcos30°+TBcos45°=TC
解得：TC=193.1N
又吊篮处于平衡状态：
故：TC=mCg
所以mC=19.3kg
答：吊篮和其中的物体总质量不应超过19.3千克．
练习册系列答案
相关题目
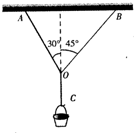在水平天花板下，两根轻绳共同悬挂一吊篮．已知AO绳与竖直方向成30°角，BO绳与 竖直方向夹角为45°，若AO绳和CO绳能承受的拉力足够大，若BO绳能承受的最大拉力为100N，求吊篮和其中的物体总质量不应超过多少千克？（结果保留一位小数）
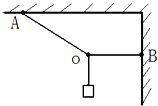如图所示，一个物体在OA、OB绳两根细绳的拉力作用下保持静止，OA绳与水平天花板间的夹角为30°，OB绳保持水平．且OA和OB绳上能承受的最大拉力均为100N，为了保证绳的安全，所挂物体的重力不得超过多少牛顿？
在水平天花板下，两根轻绳共同悬挂一吊篮．已知AO绳与竖直方向成30°角，BO绳与 竖直方向夹角为45°，若AO绳和CO绳能承受的拉力足够大，若BO绳能承受的最大拉力为100N，求吊篮和其中的物体总质量不应超过多少千克？（结果保留一位小数）