题目内容
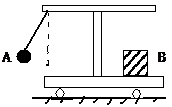
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧的形变为( )
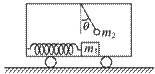
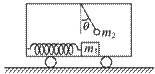
A.伸长量为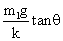 | B.压缩量为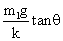 |
C.伸长量为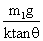 | D.压缩量为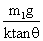 |
A
分析m2的受力情况可得:m2gtanθ=m2a,得出:a=gtanθ,再对m1应用牛顿第二定律,得:kx=m1a,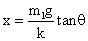 ,因a的方向向左,故弹簧处于伸长状态,故A正确.
,因a的方向向左,故弹簧处于伸长状态,故A正确.
解答本题应注意以下两点:
(1)m1和m2与小车运动状态相同.(2)隔离m1、m2分别进行受力分析,利用牛顿第二定律求解.
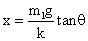 ,因a的方向向左,故弹簧处于伸长状态,故A正确.
,因a的方向向左,故弹簧处于伸长状态,故A正确. 解答本题应注意以下两点:
(1)m1和m2与小车运动状态相同.(2)隔离m1、m2分别进行受力分析,利用牛顿第二定律求解.

练习册系列答案
相关题目
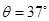 。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数
。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数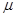 可以通过更换斜面表面的材料进行调节,调节范围是
可以通过更换斜面表面的材料进行调节,调节范围是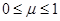 。
。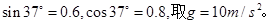

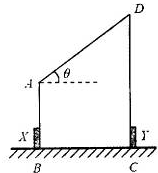
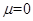 ,将P由D点静止释放,求P在斜面上的运动时间。
,将P由D点静止释放,求P在斜面上的运动时间。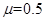 ,在A点给P一个沿斜面上的初速度
,在A点给P一个沿斜面上的初速度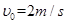 ,求P落地时的动能。
,求P落地时的动能。
 -gt
-gt