题目内容
 (2010?新都区模拟)如图所示,用长为L的轻绳把一个小铁球悬挂在高2L的O点处,小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,若运动中轻绳断开,则小铁球落到地面时的速度大小为( )
(2010?新都区模拟)如图所示,用长为L的轻绳把一个小铁球悬挂在高2L的O点处,小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,若运动中轻绳断开,则小铁球落到地面时的速度大小为( )分析:小球恰好能通过最高点B,重力提供向心力,根据牛顿第二定律和向心力公式列式求解得到B点速度;然后根据机械能守恒定律列式求解落地速度.
解答:解:小球恰好能通过最高点B,重力提供向心力,
根据牛顿第二定律,有:mg=m
①
整个运动过程只有重力做功,机械能守恒,
根据守恒定律,有:
m
+mg?3L=
mv2 ②
联立解得:v=
;
故选D.
根据牛顿第二定律,有:mg=m
| ||
| L |
整个运动过程只有重力做功,机械能守恒,
根据守恒定律,有:
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
联立解得:v=
| 7gL |
故选D.
点评:本题突破口在于小球恰好经过B点,重力提供向心力,根据牛顿第二定律列式求解速度;然后机械能守恒定律列式求解落地速度,不难.

练习册系列答案
相关题目

 (2010?新都区模拟)(1)为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶的要求的情况下,通过减少汽车后备箱中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72km/h的速度行驶时,负载改变前、后汽车受到阻力分别为2000N和1950N.请计算该方法使发动机输出功率减少了多少?
(2010?新都区模拟)(1)为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶的要求的情况下,通过减少汽车后备箱中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72km/h的速度行驶时,负载改变前、后汽车受到阻力分别为2000N和1950N.请计算该方法使发动机输出功率减少了多少?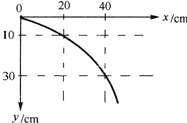 (2010?新都区模拟)在“研究平抛物体的运动”实验中
(2010?新都区模拟)在“研究平抛物体的运动”实验中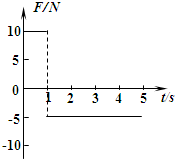 (2010?新都区模拟)如图所示,图线表示作用在某物体上的合外力跟时间变化的关系,若物体开始时是静止的,那么( )
(2010?新都区模拟)如图所示,图线表示作用在某物体上的合外力跟时间变化的关系,若物体开始时是静止的,那么( )