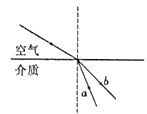
题目内容
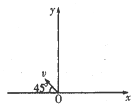
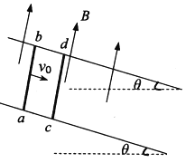
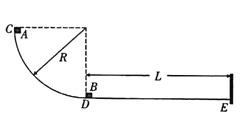
【题目】如图，半径R=0.8m的
圆弧形光滑轨道竖直放置，圆弧轨道最低点D与长为L的水平面相切于D点，质量M=1.0kg的小滑块A从圆弧顶点C由静止释放，到达最低点D后，与D点m=0.5kg的静止小物块B相碰，碰后A的速度变为vA=2.0m/s，仍向右运动。已知两物块与水平面间的动摩擦因数均为μ=0.1，A、B均可视为质点，B与E处的竖直挡板相碰时没有机械能损失，取g=10m/s2。求：
(1)碰撞后滑块B瞬间的速度大小；
(2)碰撞后瞬间B对圆弧的压力大小；
(3)要使两滑块不发生第二次碰撞，DE的长度L应满足的条件。
【答案】(1) 
(2) 
(3) 
【解析】
（1）由机械能守恒定律求出滑块的速度，两滑块碰撞过程中系统动量守恒，由动量守恒定律可以求出碰后B的速度．（2）根据牛顿第二定律求解碰撞后瞬间B对圆弧的压力大小；（3）应用动能定理求出两物块的位移，然后求出发生二次碰撞需要满足的条件．
（1）设小滑块
运动到D点的速度为
，由机械能守恒定律有
①
设B滑块被碰后的速度为
，以A的初速度方向为正方向，由动量守恒定律得
②
代入数据解得：
③
（2）
④
解得：
⑤
（3）由于B物块的速度较大，如果它们能再次相碰一定发生在B从竖直挡板弹回后，假设两物块能运动到最后停止，达到最大的路程，则对于A物块，由动能定理
⑥
代入数据解得：
⑦
对于B物块，由于B与竖直挡板的碰撞无机械能损失，由动能定理得
⑧
代入数据解得：
⑨
两滑块刚好第二次发生接触的条件
⑩
要使两滑块不发生第二次碰撞
一线名师提优试卷系列答案
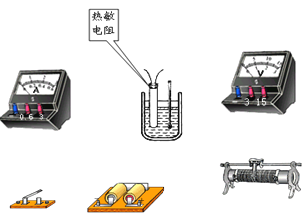
【题目】一同学测量某干电池的电动势和内阻．
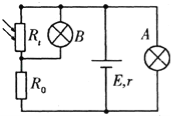
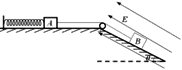
（1）如图所示是该同学正准备接入最后一根导线（图中虚线所示）时的实验电路．请指出图中在器材操作上存在的两个不妥之处__________；____________．
（2）实验测得的电阻箱阻值R和电流表示数I，以及计算的
数据见下表:
根据表中数据，在答题卡的方格纸上作出
关系图像___________．由图像可计算出该干电池的电动势为_________V；内阻为__________Ω．
R/Ω | 8.0 | 7.0 | 6.0 | 5.0 | 4.0 | |
I/A | 0.15 | 0.17 | 0.19 | 0.22 | 0.26 | |
| 6.7 | 6.0 | 5.3 | 4.5 | 3.8 |
（3）为了得到更准确的测量结果，在测出上述数据后，该同学将一只量程为100 mV的电压表并联在电流表的两端．调节电阻箱，当电流表的示数为0.33 A时，电压表的指针位置如图所示，则该干电池的电动势应为_______V；内阻应为_____Ω．
