题目内容
3.水平绳上有相距L的两个质点a、b,在某时刻a、b均处于平衡位置,且a、b之间只有一个波谷,从此时刻开始计时,经过t时间,a处第一次出现波峰,b处第一次出现波谷,则这列波的传播速度可能是( )| A. | $\frac{L}{2t}$ | B. | $\frac{L}{4t}$ | C. | $\frac{L}{6t}$ | D. | $\frac{L}{8t}$ |
分析 据题a、b均处于平衡位置,且a、b之间只有一个波谷,a、b间可能没有波峰、可能只有一个波峰,也可能有两个波峰,在此时刻a可能向上振动,也可能向下振动,根据波形确定可能的波长,根据时间确定可能的周期,即可求解波速.
解答 解:若a、b间没有波峰,此刻a点向上振动,则波长为λ=2L,$\frac{1}{4}$T=t,则周期为 T=4t,波速为v=$\frac{λ}{T}$=$\frac{2L}{4t}$=$\frac{L}{2t}$;若此刻a点向下振动,则波长为λ=2L,$\frac{3}{4}$T=t,则周期为 T=$\frac{4}{3}$t,波速为v=$\frac{λ}{T}$=$\frac{2L}{\frac{4}{3}t}$=$\frac{3L}{2t}$;
若a、b间只有一个波峰,此刻a点向上振动,则波长为λ=L,$\frac{1}{4}$T=t,则周期为 T=4t,波速为v=$\frac{λ}{T}$=$\frac{L}{4t}$;若此刻a点向下振动,则波长为λ=L,$\frac{3}{4}$T=t,则周期为 T=$\frac{4}{3}$t,波速为v=$\frac{λ}{T}$=$\frac{L}{\frac{4}{3}t}$=$\frac{3L}{4t}$;
若a、b间有两个波峰,此刻a点向上振动,则波长为λ=$\frac{2}{3}$L,$\frac{1}{4}$T=t,则周期为 T=4t,波速为v=$\frac{λ}{T}$=$\frac{\frac{2}{3}L}{4t}$=$\frac{L}{6t}$;若此刻a点向下振动,则波长为λ=$\frac{2}{3}$L,$\frac{3}{4}$T=t,则周期为 T=$\frac{4}{3}$t,波速为v=$\frac{λ}{T}$=$\frac{\frac{2}{3}L}{\frac{4}{3}t}$=$\frac{L}{2t}$;
由上可知ABC正确,D错误.
故选:ABC.
点评 解决机械波的题目关键在于明确题目中有多少种可能的状态,将所有可能情况都找出来即可正确解答.

| A. | 地球上的距离大 | B. | 月球上的距离大 | C. | 两者的距离相同 | D. | 以上说法都不对 |
| A. | 做匀变速曲线运动,每秒内速度变化的大小相等 | |
| B. | 做匀变速曲线运动,每秒内速度变化的相等 | |
| C. | 水平飞行的距离只与初速度大小有关 | |
| D. | 飞行时间只与下落的高度有关 |

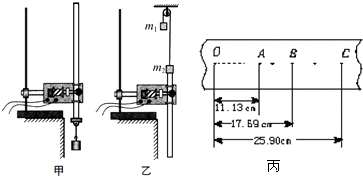
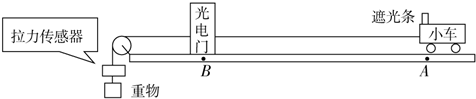
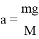 ,求出小车的加速度
,求出小车的加速度 图象,是为了便于根据图线直观地作出判断
图象,是为了便于根据图线直观地作出判断