题目内容
4.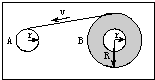 如图所示是磁带录音机的磁带盒的示意图,A,B为缠绕磁带的两个轮子,两轮的半径均为r,在放音结束时,磁带全部绕到了B轮上,磁带的外缘半径R=3r,现在进行倒带,使磁带绕到A轮上.倒带时A轮是主动轮,其角速度是恒定的,B轮是从动轮.经测定,磁带全部绕到A轮上需要的时间为t,则从开始倒带到A,B两轮的角速度相等所需要的时间( )
如图所示是磁带录音机的磁带盒的示意图,A,B为缠绕磁带的两个轮子,两轮的半径均为r,在放音结束时,磁带全部绕到了B轮上,磁带的外缘半径R=3r,现在进行倒带,使磁带绕到A轮上.倒带时A轮是主动轮,其角速度是恒定的,B轮是从动轮.经测定,磁带全部绕到A轮上需要的时间为t,则从开始倒带到A,B两轮的角速度相等所需要的时间( )| A. | 等于$\frac{t}{2}$ | B. | 大于$\frac{t}{2}$ | C. | 小于$\frac{t}{2}$ | D. | 等于$\frac{t}{3}$ |
分析 主动轮和从动轮边缘上的点线速度相等,A的角速度恒定,半径增大,线速度增大,当两轮半径相等时,角速度相等.
解答 解:在A轮转动的过程中,半径增大,角速度恒定,根据v=rω,知线速度增大,即磁带的速度逐渐增大,若磁带全部绕到A轮上需要的时间为t,则两轮半径相等前所用的时间大于半径相等后所用的时间,即A、B两轮的角速度相等所需要的时间大于$\frac{t}{2}$.故B正确,ACD错误.
故选:B.
点评 解决本题的关键知道线速度与角速度的关系,以及知道A、B两轮的角速度相等时,半径相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.了解物理规律的发现过程,学会像科学家那样观察和思考,往往比掌握知识本身更重要.下列不符合事实的是( )
| A. | 牛顿将斜面实验的结论合理外推,间接证明了自由落体运动是匀变速直线运动 | |
| B. | 开普勒发现了行星运动的规律 | |
| C. | 库仑总结出了点电荷间相互作用的规律 | |
| D. | 焦耳发现了电流热效应 |
15.2008年9月25日21时10分,“神舟”七号载人航天飞船在中国西昌卫星发射中心用“长征”二号F型火箭发射成功,9月27日翟志刚成功实施太空行走.已知“神舟”七号载人航天飞船在离地球表面h高处的轨道上做周期为T的匀速圆周运动,地球半径为R,万有引力常量为G.则( )
| A. | “神舟”七号在该轨道上运行的线速度小于第一宇宙速度 | |
| B. | “神舟”七号在该轨道上运行的向心加速度为$\frac{4{π}^{2}(R+h)}{{T}^{2}}$ | |
| C. | 地球表面的重力加速度为$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}{R}^{2}}$ | |
| D. | 若“神舟”七号升高到一个更高的轨道上做匀速圆周运动,其机械能变小(不考虑其质量变化) |
12.如图所示,所画的曲线是某电场中的三条电场线,其中有A、B、C三点,下列说法正确的是( )
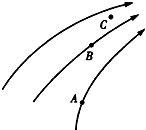

| A. | C点电势低于A点电势 | |
| B. | 由E=$\frac{F}{q}$可知,在A点放人的点电荷电荷量越大,A点的场强越小 | |
| C. | C点没有电场线通过,场强为零 | |
| D. | 电子从A点运动到B点,电场力做正功,电势能减小 |
19. P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
 P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )| A. | 离子带正电 | |
| B. | c点电势高于d点电势 | |
| C. | 离子在a点时加速度大于b点时加速度 | |
| D. | 离子在a点时电势能大于b点时电势能 |
9. 如图所示,E为电池,L是电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个规格相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
如图所示,E为电池,L是电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个规格相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
 如图所示,E为电池,L是电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个规格相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
如图所示,E为电池,L是电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个规格相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )| A. | 刚闭合S的瞬间,只有灯泡D1亮 | |
| B. | 刚闭合S的瞬间,只有灯泡D2亮 | |
| C. | 闭合S待电路达到稳定后再将S断开的瞬间,D1闪亮一下后熄灭,D2立即熄灭 | |
| D. | 闭合S待电路达到稳定后再将S断开的瞬间,D1、D2同时闪亮一下后熄灭 |
14.关于电场和磁场,下列说法正确的是( )
| A. | 某处电场的方向就是位于该处的电荷所受库仑力的方向 | |
| B. | 某处磁场的方向就是位于该处的通电导线所受安培力的方向 | |
| C. | 电荷在某处不受电场力的作用,则该处电场强度一定为零 | |
| D. | 一小段通电导线在某处不受磁场力作用,则该处磁感应强度一定为零 |

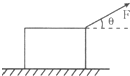 如图所示,质量m=2kg的物体静止在水平地面上,物体与水平面间的滑动摩擦力大小等于它们间弹力的0.25倍,现对物体施加一个大小F=8N、与水平方向夹角θ=37°角的斜向上的拉力,已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,质量m=2kg的物体静止在水平地面上,物体与水平面间的滑动摩擦力大小等于它们间弹力的0.25倍,现对物体施加一个大小F=8N、与水平方向夹角θ=37°角的斜向上的拉力,已知sin37°=0.6,cos37°=0.8,g取10m/s2.求: