题目内容
16.一辆质量m1=3.0×103kg的小火车因故障停在车道上,后面一辆质量m2=1.5×103kg的轿车来不及刹车,直接撞入货车尾部失去动力,相撞后两车一起沿轿车运动方向滑行了s=6.75m停下,已知车轮与路面的动摩擦因数μ=0.6,求碰撞前轿车的速度大小(重力加速度取g=10m/s2)分析 由两车碰后的运动过程由运动学公式及牛顿第二定律可求得碰后的速度;再对碰撞过程由动量守恒定律求解碰前的初速度.
解答 解:由牛顿第二定律可知:
a=$\frac{{F}_{f}}{{m}_{1}+{m}_{2}}$=μg=0.6×10=6m/s2;
由v2=2ax可得:
v=$\sqrt{2ax}$=$\sqrt{2×6×6.75}$=9m/s;
对碰撞过程设车前进方向为正方向,由动量守恒定律可得:
m2v0=(m1+m2)v
解得:v0=27m/s;
答:碰撞前轿车的速度大小为27m/s.
点评 本题考查动量守恒定律及牛顿第二定律的应用,要求能明确碰撞过程中内力远大于外力,可按动量守恒定律求解;同时注意分析物理过程;明确物理规律的选择应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图所示,一个粗细均匀的U形管内装有同种液体,液体质量为m.在管口右端用盖板A密闭,两边液面高度差为h,U形管内液体的总长度为4h,现拿去盖板,液体开始运动,由于液体受罐壁阻力作用,最终管内液体停止运动,则该过程中产生的内能为( )
如图所示,一个粗细均匀的U形管内装有同种液体,液体质量为m.在管口右端用盖板A密闭,两边液面高度差为h,U形管内液体的总长度为4h,现拿去盖板,液体开始运动,由于液体受罐壁阻力作用,最终管内液体停止运动,则该过程中产生的内能为( )
 如图所示,一个粗细均匀的U形管内装有同种液体,液体质量为m.在管口右端用盖板A密闭,两边液面高度差为h,U形管内液体的总长度为4h,现拿去盖板,液体开始运动,由于液体受罐壁阻力作用,最终管内液体停止运动,则该过程中产生的内能为( )
如图所示,一个粗细均匀的U形管内装有同种液体,液体质量为m.在管口右端用盖板A密闭,两边液面高度差为h,U形管内液体的总长度为4h,现拿去盖板,液体开始运动,由于液体受罐壁阻力作用,最终管内液体停止运动,则该过程中产生的内能为( )| A. | $\frac{1}{16}$mgh | B. | $\frac{1}{8}$mgh | C. | $\frac{1}{4}$mgh | D. | $\frac{1}{2}$mgh |
15. 远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
 远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )| A. | $\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ | B. | I2=$\frac{{U}_{2}}{R}$ | C. | I1U1>I22R | D. | I1U1=I2U2 |
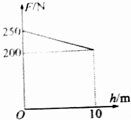 用质量为5kg的均匀铁索,从10m深的井中吊起一质量为20kg的物体,其过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10m/s2)
用质量为5kg的均匀铁索,从10m深的井中吊起一质量为20kg的物体,其过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10m/s2)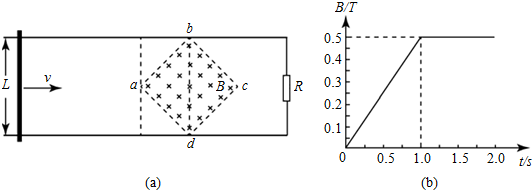
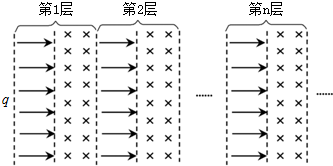
 一台质谱仪的工作原理如图所示,电荷量均为+q、质量不同的离子飘入电压为U0的加速电场,其初速度几乎为零,这些离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场,最后打在底片上,已知放置底片的区域MN=L,且OM=L.某次测量发现MN中左侧$\frac{2}{3}$区域MQ损坏,检测不到离子,但右侧$\frac{1}{3}$区域QN仍能正常检测到离子,在适当调节加速电压后,原本打在MQ的离子即可在QN检测到.
一台质谱仪的工作原理如图所示,电荷量均为+q、质量不同的离子飘入电压为U0的加速电场,其初速度几乎为零,这些离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场,最后打在底片上,已知放置底片的区域MN=L,且OM=L.某次测量发现MN中左侧$\frac{2}{3}$区域MQ损坏,检测不到离子,但右侧$\frac{1}{3}$区域QN仍能正常检测到离子,在适当调节加速电压后,原本打在MQ的离子即可在QN检测到.