题目内容
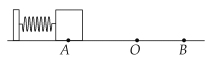
【题目】如图,轻质弹簧一端固定,另一端连接一小物块,O点为弹簧在原长时物块的位置。物块由A点静止释放,沿粗糙程度相同的水平面向右运动,最远到达B点,在从A到B的过程中,物块( )
A.加速度先减小后增大
B.经过O点时的速度最大
C.所受弹簧弹力始终做正功
D.所受弹簧弹力做的功大于克服摩擦力做的功
【答案】A
【解析】
A.由于水平面粗糙且O点为弹簧在原长时物块的位置,所以弹力与摩擦力平衡的位置在AO之间,弹力和摩擦力平衡时加速度为零,所以物块在从A到B的过程中合力先减小后增大,故加速度先减小后反向增大,故A正确;
B.物体在平衡位置处速度最大,所以物块速度最大的位置在AO之间某一位置,即在O点左侧,故B错误;
C.从A到O过程中弹力方向与位移方向相同,弹力做正功,从O到B过程中弹力方向与位移方向相反,弹力做负功,故C错误;
D.从A到B过程中根据动能定理可得
![]()
可得
![]()
即弹簧弹力做的功等于克服摩擦力做的功,故D错误。
故选A。

练习册系列答案
相关题目