题目内容
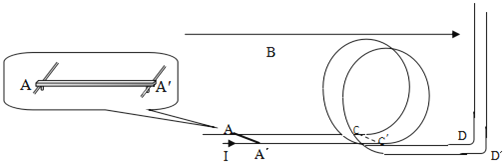
【题目】一质量m=0.05kg的金属条搁在相距d=0.02m的两金属轨道上,如图所示。现让金属条以v0=![]() m/s的初速度从AA′进入水平轨道,再由CC′进入半径r=0.05m竖直圆轨道,完成圆周运动后,再回到水平轨道上,整个轨道除圆轨道光滑外,其余均粗糙,运动过程中金属条始终与轨道垂直。已知由外电路控制,流过金属条的电流大小始终为
m/s的初速度从AA′进入水平轨道,再由CC′进入半径r=0.05m竖直圆轨道,完成圆周运动后,再回到水平轨道上,整个轨道除圆轨道光滑外,其余均粗糙,运动过程中金属条始终与轨道垂直。已知由外电路控制,流过金属条的电流大小始终为![]() =5A,方向如图中所示,整个轨道处于水平向右的匀强磁场中,磁感应强度B=1T,AC的距离L=0.2m,金属条恰好能完成竖直面里的圆周运动。试求:
=5A,方向如图中所示,整个轨道处于水平向右的匀强磁场中,磁感应强度B=1T,AC的距离L=0.2m,金属条恰好能完成竖直面里的圆周运动。试求:
(1)金属条到达竖直圆轨道最高点的速度;
(2)水平粗糙轨道的动摩擦因数;
(3)若将CC′右侧0.06m处的金属轨道在DD′向上垂直弯曲(弯曲处无能量损失),试求金属条能上升的高度。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
在最高点,抓住金属条恰好通过最高点,抓住压力为零,结合牛顿第二定理求出金属条到达竖直圆轨道最高点的速度;对开始到圆轨道的最高点过程中,运用动能定理求出水平粗糙轨道的动摩擦因数;对开始到竖直轨道的最高点过程,运用动能定理求出金属条上升的高度。
(1)金属条恰好能完成竖直面里的圆周运动,可知在最高点,对轨道的压力为零,
根据牛顿第二定律得:![]()
代入数据解得:![]()
(2)对开始到圆轨道的最高点过程中,根据动能定理得:![]()
代入数据解得:![]()
(3)对开始到最高点的过程,根据动能定理得:![]()
代入数据解得:hm=0.10m

练习册系列答案
相关题目