题目内容
【题目】如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
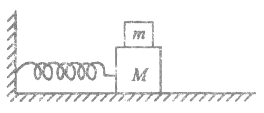
(1)使砝码随滑块一起振动的回复力是什么力?它跟位移成正比的比例常数k'等于多少?
(2)当滑块运动到振幅一半位置时,砝码所受回复力有多大?方向如何?
(3)当砝码与滑块的动摩擦因数为![]() 时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
【答案】(1)滑块对砝码的静摩擦力;![]() ; (2)
; (2)![]() ;方向指向平衡位置;(3)
;方向指向平衡位置;(3)![]()
【解析】
(1)使砝码随着滑块一起振动,砝码所受静摩擦力是产生砝码与滑块一起变加速运动的加速度.故M对m的静摩擦力是回复力.
其大小由牛顿第二定律有:f=ma
整体法求共同加速度a,则有
![]()
![]()
它跟位移成正比的比例常数
![]()
当滑块运动到振动幅的一半位置时![]() ,回复力:
,回复力:
![]()
方向指向平衡位置
(3)从f=k′x,可以看出,当x增大时,f也增大,当f=fmax=μN时,有最大振动幅,
因此
fm=mam=μmg= k′AM
要使砝码与滑块不发生相对滑动的最大振幅
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目