题目内容
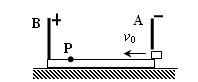
A、B两金属板如图竖直固定在绝缘底座上,与底座的总质量为m.将其静放在光滑水平面上.已知两金属板间的电压为U,极板间距为d.在A板底端上有一小孔,质量也为m、带正电、电荷量为q的小滑块以v0的速度从小孔水平滑入极板间,小滑块最远可滑到距A板为x的P点.已知小滑块与底座间的动摩擦因数为μ,极板外侧的电场强度为0.不计电场的边缘效应以及小滑块电荷对电场的影响.求:
小题1:x的值;
小题2:小滑块在极板间运动的全过程中,因与底座间的摩擦而产生的内能.

小题1:x的值;
小题2:小滑块在极板间运动的全过程中,因与底座间的摩擦而产生的内能.
小题1:
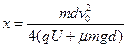
小题2:
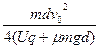
(1)(8分)解法一:
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则
由动量守恒定律得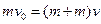 (2分)
(2分)
系统克服电场力及摩擦力做功 (3分)
(3分)
又 (1分)
(1分)
解得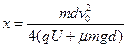 (2分)
(2分)
解法二:
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则由动量守恒定律得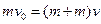 (2分)
(2分)
电容极板的电场强度 (1分)
(1分)
则小滑块所受的电场力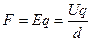
设小滑块、底座对地位移分别为 ,根据动能定理
,根据动能定理
对小滑块 (1分)
(1分)
对底座 (1分)
(1分)
解得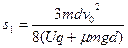 (1分)
(1分)
底座的对地位移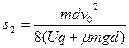 (1分)
(1分)
共速时小滑块距A板最远,最远距离
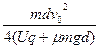 (1分)
(1分)
(2)(10分)
①当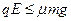 时,小滑块滑到P点后,不再相对底座滑动。 (2分)
时,小滑块滑到P点后,不再相对底座滑动。 (2分)
与底座间的摩擦而产生的内能 (2分)
(2分)
解得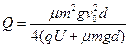 (1分)
(1分)
②当 时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)
时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)
系统克服摩擦力做功产生的热量 (2分)
(2分)
解得 (1分)
(1分)
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则
由动量守恒定律得
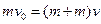 (2分)
(2分)系统克服电场力及摩擦力做功
 (3分)
(3分)又
 (1分)
(1分)解得
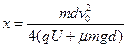 (2分)
(2分)解法二:
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则由动量守恒定律得
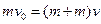 (2分)
(2分)电容极板的电场强度
 (1分)
(1分)则小滑块所受的电场力
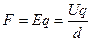
设小滑块、底座对地位移分别为
 ,根据动能定理
,根据动能定理对小滑块
 (1分)
(1分)对底座
 (1分)
(1分)解得
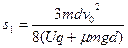 (1分)
(1分)底座的对地位移
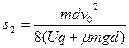 (1分)
(1分)共速时小滑块距A板最远,最远距离

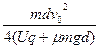 (1分)
(1分)(2)(10分)
①当
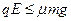 时,小滑块滑到P点后,不再相对底座滑动。 (2分)
时,小滑块滑到P点后,不再相对底座滑动。 (2分)与底座间的摩擦而产生的内能
 (2分)
(2分)解得
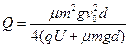 (1分)
(1分)②当
 时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)
时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)系统克服摩擦力做功产生的热量
 (2分)
(2分)解得
 (1分)
(1分)
练习册系列答案
相关题目
 =53°的光滑斜面顶端A并沿斜面下滑,斜面底端B与光滑水平轨道平滑连接,小球以不变的速率过B点后进入BC部分,再进入竖直圆轨道内侧运动.已知斜面顶端与平台的高度差h=3.2m,斜面顶端高H=15m,竖直圆轨道半径R=5m. g取10m/s2.试求:
=53°的光滑斜面顶端A并沿斜面下滑,斜面底端B与光滑水平轨道平滑连接,小球以不变的速率过B点后进入BC部分,再进入竖直圆轨道内侧运动.已知斜面顶端与平台的高度差h=3.2m,斜面顶端高H=15m,竖直圆轨道半径R=5m. g取10m/s2.试求:
 及斜面顶端与平台边缘的水平距离x;
及斜面顶端与平台边缘的水平距离x;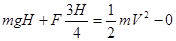 ,解方程得到V的大小。
,解方程得到V的大小。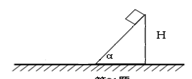


 L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求:
L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求: