Question

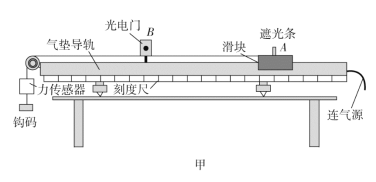
【题目】如图所示，在水平桌面上放有长木板C，C上右端是固定挡板P，在C上左端和中点处各放有小物块A和B，A、B的尺寸以及P的厚度皆可忽略不计，刚开始A、B之间和B、P之间的距离皆为L。设木板C与桌面之间无摩擦，A、C之间和B、C之间的动摩擦因数均为，且最大静摩擦力等于滑动摩擦力；A、B、C（连同挡板P）的质量相同．开始时，B和C静止，A以某一初速度向右运动．假设所有的碰撞都是弹性正碰。

（1）若物块A与B恰好发生碰撞，求A的初速度；

（2）若B与挡板P恰好发生碰撞，求A的初速度；

（3）若最终物块A从木板上掉下来，物块B不从木板C上掉下来，求A的初速度的范围。

Answer 1

【答案】（1）（2）（3）

【解析】

（1）若物块刚好与物块不发生碰撞，则物块运动到物块所在处时，与的速度大小相等．因为物块与木板的速度相等，所以此时三者的速度均相同，设为，由动量守恒定律得

在此过程中，整个系统动能的改变等于系统内部相互间的滑动摩擦力做功的代数和，即

解得

故与恰好发生碰撞的条件是：

（2）物块、发生碰撞的极短时间内，与构成的系统的动量守恒，而木板的速度保持不变．因为物块、间的碰撞是弹性的，系统的机械能守恒，又因为质量相等，由动量守恒和机械能守恒，碰撞前后、交换速度，若碰撞刚结束时，、、三者的速度分别为、和，则有

若物块刚好与挡板不发生碰撞，则物块以速度从板板的中点运动到挡板所在处时，与的速度相等．因与的速度大小是相等的，故、、三者的速度相等，设此时三者的速度为．根据动量守恒定律有：

整个系统动能的改变，等于系统内部相互问的滑动摩擦力做功的代数和，即

解得

即物块的初速度时，与刚好发生碰撞

（3） 若恰好没从木板上掉下来，即到达的左端时的速度变为与相同，这时三者的速度皆相同，以表示，由动量守恒有：

从以初速度在木板的左端开始运动，经过与相碰，直到刚没从木板的左端掉下来，这一整个过程中，系统内部先是相对的路程为；接着相对运动的路程也是；与碰后直到刚没从木板上掉下来，与相对运动的路程也皆为．整个系统动能的改变应等于

内部相互间的滑动摩擦力做功的代数和，即

得

故从上掉下的条件是

设刚要从木板上掉下来时，、、三者的速度分别为、和，则有 ，此时有

当物块从木板上掉下来后，若物块刚好不会从木板上掉下，即当的左端赶上时，与的速度相等．设此速度为，则对、这一系统来说，由动量守恒定律，有

在此过程中，对这一系统来说，滑动摩擦力做功的代数和为，由动能定理可得

解得

故物块不从木板上掉下来的条件是;

综上所述，A的初速度范围是