题目内容
【题目】如图所示，M、N为中心开有小孔的平行板电容器的两极板，相距为D，其右侧有一边长为2a的正三角形区域，区域内有垂直纸面向里的匀强磁场，在极板M、N之间加上电压U后，M板电势高于N板电势.现有一带正电的粒子，质量为m，电荷量为q，其重力和初速度均忽略不计，粒子从极板M的中央小孔S1处射入电容器，穿过小孔S2后从距三角形A点
a的P处垂直AB方向进入磁场，试求：
(1)粒子到达小孔S2时的速度；
(2)若粒子能从AC间离开磁场，磁感应强度应满足什么条件？
【答案】(1) 
（2）
≤B＜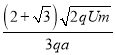
【解析】(1) 带电粒子在电场中运动时由动能定理得： 
，解得粒子进入磁场时的速度大小为
；
(2) 粒子从进入磁场到从AC间离开，若粒子恰能到达BC边界，如图所示，
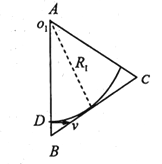
设此时的磁感应强度为B1，根据几何关系有此时粒子的轨道半径为
，由牛顿第二定律可得
，由以上两式解得
，
粒子从进入磁场到从AC间离开，若粒子恰能到达AC边界，如图所示，
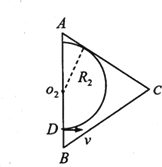
设此时的磁感应强度为B2，根据几何关系有： 
，由牛顿第二定律可得： 
，
由以上两式解得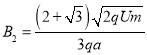
，总上所述要使粒子能从AC间离开磁场，磁感应强度应满足： 
。
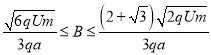练习册系列答案
能考试期末冲刺卷系列答案
相关题目
