题目内容
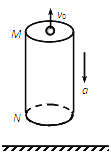
【题目】如图所示,离地面足够高处有一竖直空管,质量为2 kg,管长24 m,M、N为空管的上、下两端,空管受到竖直向上的拉力作用,由静止开始竖直向下做加速运动,加速度大小为a=2 m/s2,同时在M处一个大小不计的小球沿管的轴线以初速度v0竖直上抛,不计一切阻力,取重力加速度g=10 m/s2。
(1)若小球上抛的初速度大小为10 m/s,经过多长时间小球从管的N端穿出?
(2)若此空管的N端距离地面64 m高,欲使在空管到达地面时小球落到管内,求小球的初速度v0大小的取值范围。
【答案】(1)4 s (2)29 m/s≤v0≤32 m/s
【解析】(1)以向下为正方向,设经t时间,小球从N端穿出
小球下落的高度h1=–v0t+![]() gt2
gt2
空管下落的高度h2=![]() at2
at2
又h1–h2=L
联立有–v0t+![]() gt2–
gt2–![]() at2=L
at2=L
代入数据解得t=4 s(另解t=–1.5 s舍去)
(2)设空管经t′时间到达地面,则H=![]() at′2
at′2
可得t'=![]() =8 s
=8 s
小球在t′时间下落的高度h=–v0t′+![]() gt′2
gt′2
小球落入管内的条件是64 m≤h≤88 m
解得29 m/s≤v0≤32 m/s

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目