Question

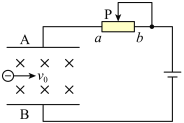
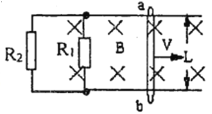
【题目】如图所示，水平放置的平行金属导轨，相距L=0.5m，左端接一电阻R1=0.30Ω，R1=0.60Ω，磁感应强度B=0.40T的匀强磁场方向垂直导轨平面，导体棒ab的 电阻为r=0.20Ω，垂直导轨放在导轨上，导轨的电阻均可忽略不计，当ab棒以V=4.Om/s的速度水平向右滑动时，求：

（1）ab棒中感应电动势；

（2）回路中感应电流的大小；

（3）ab两点的电势差。

（4）求整个电路的发热功率和R2的发热功率。

Answer 1

【答案】（1）0.80V（2）2A（3）0.04V（4）l.6W ；0.27W

【解析】

由导体棒切割磁感线产生电动势的公式E=BLv求解感应电动势；由闭合电路殴姆定律即可求出回路中的电流；根据欧姆定律求解ab两端的电压。根据P总=EI求总功率。

（1）由法拉第电磁感应定律得：E=BLv=0.40×0.5×4.0V=0.80V

（2）整个电路的总电阻为

所以回路中感应电流大小为

（3）ab两点的电势差：

（4）整个电路的发热功率为P总=EI=0.80×2W=l.6W

R2的发热功率为：P=