��Ŀ����
����Ŀ���뾶ΪR��ˮƽԲ̨������ͨ��Բ��O����ֱ�⻬ϸ��CC��ת������ͼ��ʾ��Բ̨�������ֱ�������뾶������а��ۣ�����ΪmA������A����һ�����ڣ�����A��۵�Ķ�Ħ������Ϊ�̣�����ΪmB������B������һ�����ڣ��˲��ǹ⻬�ģ�AB����һ��Ϊl��l��R���Ҳ����쳤�������ƹ�ϸ����������֪Բ̨������ת������A��B���������Բ̨������A��B���������Ϊ�ʵ㣬��������Ħ�������Ƶ��ڻ���Ħ��������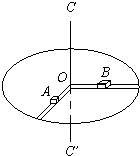
��1����Բ̨ת���Ľ��ٶ�Ϊ��0 �� OA�ij���Ϊl1ʱ����д��A��B���������ܵ�����������С�ı���ʽ��
��2������Բ̨ת���Ľ��ٶ�Ϊ���Ҫʹ����A�Ͳ�֮��ǡ��û��Ħ��������OA�ij�Ϊ���
��3����OA��Ϊx���Է���Բ̨�Ľ��ٶȦغ�����A��Բ�ĵľ���x��Ӧ�����������
���𰸡�
��1��
�⣺����������ʽ�ɵã�
A��������С�ı���ʽ��FA=mA��02l1
B����������FB=mB��02��l��l1��
��2��
�⣺��OA��Ϊl1����OBΪl��l1��
F=mA��2l1
F=mB��2��l��l1��
��� ![]()
��3��
�⣺��A��B���������ת̨��ֹ��ǡ��Ħ��ʱ������A��B�Ķ���ѧ���̷ֱ�Ϊ
F=mA��2x��F=mB��2��l��x����������� ![]()
��A��B���������ת̨��ֹ��Aǡû����Զ�����ĵ��˶�ʱ������A��B�Ķ���ѧ���̷ֱ�Ϊ
F+��mAg=mA��2x��F=mB��2��l��x��
![]() ��
�� ![]()
��A��B���������ת̨��ֹ��Aǡû���������ĵ��˶�ʱ������A��B�Ķ���ѧ���̷ֱ�Ϊ
F����mAg=mA��2x��F=mB��2��l��x��
![]() ��
�� ![]()
���Ϸ�����֪
����������1����֪ת�����ٶȣ��������֪�������ת���뾶������������ʽ�������������С�ı���ʽ����2��ҪʹA����Ħ������Ӧʹ���ӵ������䵱�����������������������Ҫ����������ȣ�������ʽ�ɽ�þ��룻��3���ɷ�Ϊ������ǡ��Ħ������Aǡ�ôﵽ���Ħ������Bǡ�ôﵽ���Ħ�������������������ţ�ٵڶ����ɿɵó����ٶȼ�����Ŀ���ֵ��
�����㾫����ͨ�������������������������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�������������Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�