题目内容
如图所示为闭合电路中的一部分导体ab在磁场中做切割磁感线运动的情景，其中能产生由a到b的感应电流的是（ ）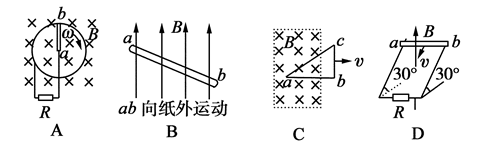
A
解析试题分析：图A中产生的感应电流方向是由a向b。原因是:在A中，由于穿过电路的磁感线数目是增加的，根据楞次定律可知，感应磁场的方向与磁感线方向相反，再根据右手螺旋法则（也称安培定则）可知，电路中产生的感应电流由a向b，所以A正确；在图B中，虽然导体ab切割磁感线，但它不是闭合电路的一部分，所以只会产生感应电动势，而不会产生感应电流，所以B错误；在图C中，由于三角形向右切割磁感线运动，穿过三角形的磁感线数目减少，根据楞次定律可知，感应磁场方向与图中磁感线方向相同，再根据右手螺旋法则（也称安培定则）可知电路中产生的感应电流方向由b向a所以C错误；在图D中，用右手定则可判断出导体ab中产生的感应电流的方向是由b向a的，所以D错误。
考点：本题考查电磁感应产生的条件判断
一种早期发电机原理示意图如图所示，该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成，两磁极相对于线圈平面对称，线圈圆心为O点。在磁极绕转轴匀速转动的过程中，当磁极与O点在同一条直线上时，穿过线圈的
| A．磁通量最大，产生的感应电流最大 |
| B．磁通量最大，产生的感应电流最小 |
| C．磁通量最小，产生的感应电流最大 |
| D．磁通量最小，产生的感应电流最小 |
如下图所示，两根光滑的金属导轨，平行放置在倾角为θ的斜面上，导轨的左端接有电阻R，导轨自身的电阻可忽略不计．斜面处在一匀强磁场中，磁场方向垂直于斜面向上．质量为m、电阻不计的金属棒ab，在沿着斜面与棒ab垂直的恒力F作用下沿导轨匀速上升，上升高度为h.则在此过程中，以下错误的是( )
| A．作用于棒ab上的各力的合力所做的功等于零 |
| B．恒力F和重力的合力所做的功等于电阻R上产生的焦耳热 |
| C．恒力F和安培力的合力所做的功等于零 |
| D．恒力F所做的功等于棒ab重力势能的增加量和电阻R上产生的焦耳热之和 |
如图所示,a、b、c三个闭合线圈,放在同一平面内,当a线圈中有电流I通过时,它们的磁通量分别为Фa、Фb、Фc下列说法中正确的是( )
| A．Фa＜Фb＜Фc | B．Фa＞Фb＞Фc |
| C．Фa＜Фc＜Фb | D．Фa＞Фc＞Фb |
如图所示，在水平面内的直角坐标系xOy中有一光滑固定金属导轨AOC，其中曲线导 轨OA满足方程y="isinkx" ，0C导轨与x轴重合,整个导轨处于竖直向上的勻强磁场中。现有一单位长度的电阻为R0，长为L的直金属棒从图示位置开始沿x轴正方向匀速运动
距离。不计金属导轨A0C电阻和所有接触电阻，则在该直金属棒运动过程中，它与导轨组成的闭合回路
| A．感应电流沿逆时针方向 |
| B．感应电动势与进入轨道距离-成正比 |
| C．感应电流大小和方向均不变 |
| D．电功率不变 |
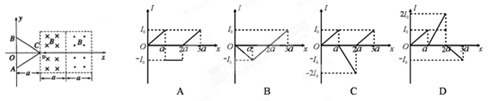
如图甲所示，在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4，在L1L2之间和L3L4之间存在匀强磁场，磁感应强度B大小均为1T，方向垂直于虚线所在平面。现有一矩形线圈abcd，宽度cd＝L＝0.5m，质量为0.1kg，电阻为2Ω，将其从图示位置由静止释放(cd边与L1重合)，速度随时间的变化关系如图乙所示，t1时刻cd边与L2重合，t2时刻ab边与L3重合，t3时刻ab边与L4重合，已知t1～t2的时间间隔为0.6s，整个运动过程中线圈平面始终处于竖直方向，重力加速度g取10m/s2。则
| A．在0～t1时间内，通过线圈的电荷量为0.25C |
| B．线圈匀速运动的速度大小为8m/s |
| C．线圈的长度为1m |
| D．0～t3时间内，线圈产生的热量为4.2J |
如图线框在匀强磁场中绕OO,轴匀速转动(由上向下看是逆时针方向)，从图示位置继续转动到线框与匀强磁场垂直的过程中，磁通量和感应电动势大小的变化情况是（ ）
| A．磁通量和感应电动势都在变大 |
| B．磁通量和感应电动势都在变小 |
| C．磁通量在变小，感应电动势在变大 |
| D．磁通量在变大，感应电动势在变小 |