题目内容
4.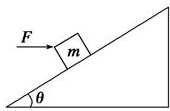 如图所示,质量为m=1.1kg的小物块P从倾角为θ=37°的固定斜面上释放后,能沿足够长斜面下滑,已知物块与斜面的摩擦因数为μ=0.5,重力加速度为g=10m/s2,试求:
如图所示,质量为m=1.1kg的小物块P从倾角为θ=37°的固定斜面上释放后,能沿足够长斜面下滑,已知物块与斜面的摩擦因数为μ=0.5,重力加速度为g=10m/s2,试求:(1)物块静止释放后,下滑过程的加速度a;
(2)若在物体下滑过程中,某时刻受到水平向右的力F=3N作用,求F作用瞬间的加速度;
(3)若物体以初速度v0沿斜面上滑的过程中,某时刻受到水平向右的力F=3N作用,求F作用瞬间的加速度.
分析 (1)运用牛顿第二定律求物块下滑的加速度a.
(2)F作用的瞬间,物块仍向下滑动,摩擦力的方向不变,根据牛顿第二定律,由正交分解法求瞬间的加速度.
(3)若物体以初速度v0沿斜面上滑的过程中,所受的滑动摩擦力沿斜面向下,再由牛顿第二定律求F作用瞬间的加速度.
解答  解:(1)对物块,由牛顿第二定律得:
解:(1)对物块,由牛顿第二定律得:
mgsin37°-μmgcos37°=ma
得:a=g(sin37°-μcos37°)=10×(0.6-0.5×0.8)=2m/s2,方向沿斜面向下
(2)F作用的瞬间,物块受力情况如右图所示.取沿斜面向上为正方向,由牛顿第二定律得:
Fcosθ+f-mgsinθ=ma1;
Fsinθ+mgcosθ-N=0;
又 f=μN
联立解得 a1=$\frac{F(cosθ-μsinθ)}{m}$-g(sin37°-μcos37°)=$\frac{3×(0.8-0.5×0.6)}{1.1}$-2=-$\frac{7}{11}$m/s2,负号表示方向沿斜面向下.
(3)若物体以初速度v0沿斜面上滑的过程中,所受的滑动摩擦力沿斜面向下,F作用的瞬间,取沿斜面向上为正方向,由牛顿第二定律得:
Fcosθ-f-mgsinθ=ma1;
Fsinθ+mgcosθ-N=0;
又 f=μN
联立解得 a1=$\frac{F(cosθ-μsinθ)}{m}$-g(sin37°+μcos37°)=$\frac{3×(0.8-0.5×0.6)}{1.1}$-10×(0.6+0.5×0.8)=-$\frac{95}{11}$m/s2,负号表示方向沿斜面向下.
答:
(1)物块静止释放后,下滑过程的加速度a为2m/s2.方向沿斜面向下.
(2)F作用瞬间的加速度大小为$\frac{7}{11}$m/s2,方向沿斜面向下.
(3)F作用瞬间的加速度大小为$\frac{95}{11}$m/s2,方向沿斜面向下.
点评 本题是牛顿第二定律的基本运用,要在正确分析受力的基础上,运用正交分解法,由牛顿第二定律求加速度,要注意加速度的方向.

 如图所示,在竖直平面内有半径为R和1.5R的两个圆,两圆的最高点相切,切点为a,b和c分别是小圆和大圆上的两个点,其中ab长为1.6R,ac长为3R.现沿ab和ac建立两条光滑轨道,自a处由静止释放小球,已知小球沿ab轨道运动到b点所用时间为t1,沿ac轨道运动到c点所用时间为t2,则t1与t2之比为( )
如图所示,在竖直平面内有半径为R和1.5R的两个圆,两圆的最高点相切,切点为a,b和c分别是小圆和大圆上的两个点,其中ab长为1.6R,ac长为3R.现沿ab和ac建立两条光滑轨道,自a处由静止释放小球,已知小球沿ab轨道运动到b点所用时间为t1,沿ac轨道运动到c点所用时间为t2,则t1与t2之比为( )| A. | 2:3 | B. | 5:8 | C. | 15:16 | D. | $\sqrt{2}:\sqrt{3}$ |
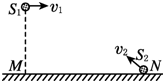 在水平地面上M点的正上方80m处,将S1球以初速度v1=30m/s水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,且S2球的速度变化量为20m/s,不计空气阻力,g=10m/s2,则两球从抛出到相遇过程中,下列说法错误的是( )
在水平地面上M点的正上方80m处,将S1球以初速度v1=30m/s水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,且S2球的速度变化量为20m/s,不计空气阻力,g=10m/s2,则两球从抛出到相遇过程中,下列说法错误的是( )| A. | 两球的速度变化量相等 | |
| B. | 抛出S2球的初速度方向与水平地面的夹角为37° | |
| C. | MN的距离为60m | |
| D. | 两个小球都做匀变速运动 |
 如图所示,虚线所示的区域内,有方向垂直于纸面向里的匀强磁场,从边缘A处有一束速度各不相同的质子沿半径方向射入磁场,这些质子在磁场区运动过程中( )
如图所示,虚线所示的区域内,有方向垂直于纸面向里的匀强磁场,从边缘A处有一束速度各不相同的质子沿半径方向射入磁场,这些质子在磁场区运动过程中( )| A. | 运动时间越长,其轨迹越长 | |
| B. | 运动时间越长,其轨迹对应的圆心角越大 | |
| C. | 运动时间越长,射出的速率越大 | |
| D. | 运动时间越长,射出磁场时速度方向偏转角越大 |
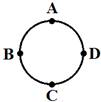 如图所示,两人同时从圆上A点出发,分别沿圆弧ABC和直径AC行走,最后在C点相遇,则两人从出发到相遇的过程中相同的物理量是( )
如图所示,两人同时从圆上A点出发,分别沿圆弧ABC和直径AC行走,最后在C点相遇,则两人从出发到相遇的过程中相同的物理量是( )| A. | 路程 | B. | 相遇时瞬时速度 | C. | 平均速率 | D. | 平均速度 |
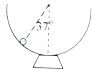 如图在光滑半球型碗中,有一带电+q=3×10-2C质量m=0.4kg的小球,在水平向左的匀强电场中静止在与竖直方向偏左37°位置处,问匀强电场的大小是多少?(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图在光滑半球型碗中,有一带电+q=3×10-2C质量m=0.4kg的小球,在水平向左的匀强电场中静止在与竖直方向偏左37°位置处,问匀强电场的大小是多少?(g=10m/s2,sin37°=0.6,cos37°=0.8)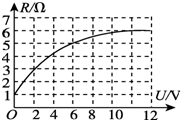 一个标有“12V”字样、功率未知的灯泡,测得灯丝电阻R随灯泡两端电压变化的关系图线如图所示,利用这条图线计算:
一个标有“12V”字样、功率未知的灯泡,测得灯丝电阻R随灯泡两端电压变化的关系图线如图所示,利用这条图线计算: 如图所示,质量为m、内壁光滑的半圆形轨道静止在水平地面上,O为其圆心,P为轨道上一点,其中OP与OA的夹角为θ.将一质量为m的小物块由图中的A点处静止释放.求:
如图所示,质量为m、内壁光滑的半圆形轨道静止在水平地面上,O为其圆心,P为轨道上一点,其中OP与OA的夹角为θ.将一质量为m的小物块由图中的A点处静止释放.求: