题目内容
9.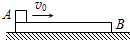 如图所示,一质量为M=4kg、长为L的长方形木板B放在光滑水平地面上,在其左端放一质量为m=1kg的小木块A.现以地面为参照系,给A一向右的初速度(见图),使A开始向右运动,最后A刚好没有离开B板.
如图所示,一质量为M=4kg、长为L的长方形木板B放在光滑水平地面上,在其左端放一质量为m=1kg的小木块A.现以地面为参照系,给A一向右的初速度(见图),使A开始向右运动,最后A刚好没有离开B板.(1)若已知A的初速度大小为v0=2m/s,求它们最后的速度大小和方向.
(2)若小木块A与木板B之间的动摩擦因数为?=0.1,求木板B的长度L.
分析 (1)根据动量守恒定律求出最后的速度大小和方向.
(2)根据能量守恒求出木板B的长度.
解答 解:(1)A、B组成的系统动量守恒,规定向右为正方向,根据动量守恒定律得,
mv0=(M+m)v,
解得$v=\frac{m{v}_{0}}{M+m}=\frac{1×2}{4+1}m/s=0.4m/s$,方向向右.
(2)根据能量守恒得,$μmgL=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}(M+m){v}^{2}$,
代入数据解得L=1.6m.
答:(1)它们最后的速度大小为0.4m/s,方向向右.
(2)木板B的长度为1.6m.
点评 本题运用动量守恒和能量守恒定律进行求解比较简捷,也可以抓住A做匀减速运动,B做匀加速运动,速度相等时A恰好滑动B的右端,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
19. 在半球形光滑容器内,放置一细杆,如图所示,细杆与容器的接触点分别为A、B两点,则容器上A、B两点对细杆的作用力方向分别为( )
在半球形光滑容器内,放置一细杆,如图所示,细杆与容器的接触点分别为A、B两点,则容器上A、B两点对细杆的作用力方向分别为( )
 在半球形光滑容器内,放置一细杆,如图所示,细杆与容器的接触点分别为A、B两点,则容器上A、B两点对细杆的作用力方向分别为( )
在半球形光滑容器内,放置一细杆,如图所示,细杆与容器的接触点分别为A、B两点,则容器上A、B两点对细杆的作用力方向分别为( )| A. | 均竖直向上 | B. | 均指向球心 | ||
| C. | A点处指向球心O,B点处竖直向上 | D. | A点处指向球心O,B点处垂直于细杆 |
4.如图为一根张紧的绳子上系着五个单摆,让A摆先摆动起来,各摆的摆动情况正确的是( )


| A. | C摆的振幅最大 | B. | E摆的振幅最大 | ||
| C. | B摆振动周期最小 | D. | 各摆的振动周期相等 |
1.下面对某原子核衰变的描述中正确的是( )
| A. | 放出一个β粒子后,原子核的中子数减少1,原子序数少1 | |
| B. | 放出一个β粒子后,原子核的质量数不变,中子数减少1,质子数增加1 | |
| C. | 放出一个α粒子后,原子核的质量数少4,电荷数少2 | |
| D. | γ射线是处于较高能级的原子核向低能级跃迁时释放的能量 |
18. 公元1543年,哥白尼的著作《天体运行论》正式发表,该书中提出行星绕太阳做匀速圆周运动,6颗行星运动的示意图如图所示.假设行星只受到太阳的引力,按照哥白尼上述的观点.下列说法中正确的是( )
公元1543年,哥白尼的著作《天体运行论》正式发表,该书中提出行星绕太阳做匀速圆周运动,6颗行星运动的示意图如图所示.假设行星只受到太阳的引力,按照哥白尼上述的观点.下列说法中正确的是( )
 公元1543年,哥白尼的著作《天体运行论》正式发表,该书中提出行星绕太阳做匀速圆周运动,6颗行星运动的示意图如图所示.假设行星只受到太阳的引力,按照哥白尼上述的观点.下列说法中正确的是( )
公元1543年,哥白尼的著作《天体运行论》正式发表,该书中提出行星绕太阳做匀速圆周运动,6颗行星运动的示意图如图所示.假设行星只受到太阳的引力,按照哥白尼上述的观点.下列说法中正确的是( )| A. | 太阳对6颗行星的引力一样大 | |
| B. | 6颗行星中,水星绕太阳运动的角速度最小 | |
| C. | 6颗行星中,土星绕太阳运动的向心加速度最大 | |
| D. | 火星绕太阳运动的周期大于一年 |
 如图所示,是一传送装置,其中AB段粗糙,AB段长为L=1m,动摩擦因数u=0.5,BC、DEN段均可视为光滑,DEN是半径为r=0.5m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.其中N点又与足够长的水平传送带的右端平滑对接,传送带以4m/s的速率沿顺时针方向匀速转动,小球与传送带之间的动摩擦因数也为0.5.左端竖直墙上固定有一轻质弹簧,现用一可视为质点的小球压缩弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿圆弧DEN轨道滑下,而始终不脱离轨道.已知小球质量m=0.2kg,g取10m/s2.
如图所示,是一传送装置,其中AB段粗糙,AB段长为L=1m,动摩擦因数u=0.5,BC、DEN段均可视为光滑,DEN是半径为r=0.5m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.其中N点又与足够长的水平传送带的右端平滑对接,传送带以4m/s的速率沿顺时针方向匀速转动,小球与传送带之间的动摩擦因数也为0.5.左端竖直墙上固定有一轻质弹簧,现用一可视为质点的小球压缩弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿圆弧DEN轨道滑下,而始终不脱离轨道.已知小球质量m=0.2kg,g取10m/s2. 地面上放一木箱,质量为40kg,用100N的力与水平成37°角推木箱,如图所示,恰好使木箱匀速前进.若用此力与水平成37°角向斜上方拉木箱,木箱的加速度多大?
地面上放一木箱,质量为40kg,用100N的力与水平成37°角推木箱,如图所示,恰好使木箱匀速前进.若用此力与水平成37°角向斜上方拉木箱,木箱的加速度多大? 已知两电阻R1=4Ω,R2=6Ω,则他们并联后的总电阻为2.4Ω,串联后的总电阻为10Ω,若两电阻并联后接在4.8V的电源两段(如图所示,电源内阻不计),通过R1的电流为1.2 A.
已知两电阻R1=4Ω,R2=6Ω,则他们并联后的总电阻为2.4Ω,串联后的总电阻为10Ω,若两电阻并联后接在4.8V的电源两段(如图所示,电源内阻不计),通过R1的电流为1.2 A.