题目内容
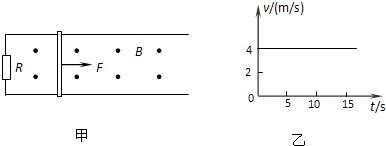
（13分）如图甲所示，两根足够长的光滑平行金属导轨相距为L＝0.40m，导轨平面与水平面成q＝30°角，上端和下端通过导线分别连接阻值R1＝R2＝1.2W的电阻，质量为m＝0.20kg、阻值为r＝0.20W的金属棒ab放在两导轨上，棒与导轨垂直且保持良好接触，整个装置处在垂直导轨平面向上的磁场中，取重力加速度g＝10 m/s2。若所加磁场的磁感应强度大小恒为B，通过小电动机对金属棒施加力，使金属棒沿导轨向上做匀加速直线运动，经过0.5s电动机的输出功率达到10W，此后保持电动机的输出功率不变，金属棒运动的v－t图如图乙所示，试求：
（1）磁感应强度B的大小；
（2）在0－0.5s时间内金属棒的加速度a的大小；
（3）在0－0.5s时间内电动机牵引力F与时间t的关系；
（4）如果在0－0.5 s时间内电阻R1产生的热量为0.135 J，则这段时间内电动机做的功。
13分）
（1）
＝mg sin30°＋
，B＝1 T， （2＋1＝3分）
（2）
－mg sin30°－
＝ma，a＝
m/s2， （2＋1＝3分）
（3）F－mg sin30°－＝ma，F＝
t＋
， （2＋1＝3分）
（4）Q1＝（
）2´1.2＝0.3I2，Qr＝0.2I2，Q总＝2Q1＋Qr＝0.36 J， （1分）
WF－Q总－
mgat12 sin30°＝m（at1）2， （2分）
所以WF＝Q总＋mgat12 sin30°＋m（at1）2＝3.97 J。 （1分）
练习册系列答案
相关题目
求：
如图甲所示，两根足够长的平行光滑金属导轨固定放置在水平面上，间距L=0.2m，一端通过导线与阻值为R=1Ω的电阻连接；导轨上放一质量为m=0.5kg的金属杆，金属杆与导轨的电阻均忽略不计．整个装置处于竖直向上的大小为B=0.5T的匀强磁场中．现用与导轨平行的拉力F作用在金属杆上，金属杆运动的v-t图象如图乙所示．（取重力加速度g=10m/s2）求：
如图甲所示，两根足够长的平行导轨处在与水平方向成θ角的斜面上，θ=370，导轨电阻不计，间距L=0.3m．在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场．导轨底端接一个阻值R=1Ω的电阻．质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间，棒与导轨间的动摩擦因数μ=0.5，金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑，滑至最高点时高度为h2=3.2m，sin37°=0.6，cos37°=0.8，取g=10m/s2．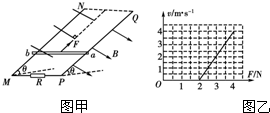
如图甲所示，两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L．M、P两点间接有阻值为R的电阻．一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直．整套装置处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下．导轨和金属杆的电阻可忽略．用与导轨平行且向上的恒定拉力F作用在金属杆上，金属杆ab沿导轨向上运动，最终将做匀速运动．当改变拉力F的大小时，相对应的匀速运动速度v也会改变，v和F的关系如图乙所示．