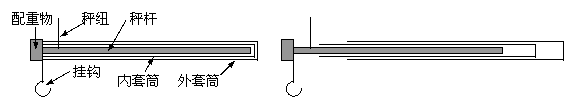题目内容
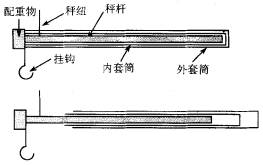
有人设计了一种新型伸缩拉杆秤.结构如图,秤杆的一端固定一配重物并悬一挂钩,秤杆外面套有内外两个套筒,套筒左端开槽使其可以不受秤纽阻碍而移动到挂钩所在的位置(设开槽后套筒的重心仍在其长度中点位置).秤杆与内层套筒上刻有质量刻度.空载(挂钩上不挂物体,且套筒未拉出)时.用手提起秤纽,杆杆秤恰好平衡.当物体挂在挂钩上时,往外移动内外套筒可使杆秤平衡,从内外套筒左端的位置可以读得两个读数,将这两个读数相加,即可得到待测物体的质量.已知秤杆和两个套稠的长度均为16cm,套筒可移出的最在距离为15cm,秤纽到挂钩的距离为2cm,两个套筒的质量均为0.1kg.取重力加速度g=9.8m/s2.求:
(1)当杆秤空载时,秤杆、配重物及挂钩所受重力相对秤纽的合力矩;
(2)当在秤钩上挂一物体时,将内套筒向右移动5cm,外套筒相对内套筒向右移动8cm,杆秤达到平衡,物体的质量多大?
(3)若外层套筒不慎丢失,在称某一物体时,内层套筒的左端在读数为1kg外杆恰 好平衡,则该物体实际质量多大?

(1)当杆秤空载时,秤杆、配重物及挂钩所受重力相对秤纽的合力矩;
(2)当在秤钩上挂一物体时,将内套筒向右移动5cm,外套筒相对内套筒向右移动8cm,杆秤达到平衡,物体的质量多大?
(3)若外层套筒不慎丢失,在称某一物体时,内层套筒的左端在读数为1kg外杆恰 好平衡,则该物体实际质量多大?

分析:(1)根据平衡时两套筒的重力相对秤纽的力矩与所求的合力矩相等求解.
(2)由物体的力矩与内外套筒增加的力矩之和平衡求出.
(3)正常称量重物时,内外套筒可一起向外拉出,由力矩平衡求出内外套筒可一起向外拉出,再由力矩平衡求解物体实际质量.
(2)由物体的力矩与内外套筒增加的力矩之和平衡求出.
(3)正常称量重物时,内外套筒可一起向外拉出,由力矩平衡求出内外套筒可一起向外拉出,再由力矩平衡求解物体实际质量.
解答:解:(1)由题意:套筒不拉出时杆称恰好平衡,此时两套筒的重力相对秤纽的力矩与所求的合力矩相等,设套筒长度为L,
则所求合力矩M=2mg(
-d)=2×0.1×10(0.08-0.02)Nm=0.12N?m,
(2)由力矩平衡得
m1gd=mgx1+mg(x1+x2)
解得m1=
m=
×0.1kg=0.9kg.
(3)正常称量1kg重物时,内外套筒可一起向外拉出x′
由力矩平衡得 m2′gd=2mgx′,x′=
d=0.1m
外套筒丢失后,此时内套筒左端离称纽距离为x′-d=0.08m
由力矩平衡
m2gd+M=mg(x′-d+
)
解得m2=0.2kg
答:(1)当杆秤空载时,秤杆、配重物及挂钩所受重力相对秤纽的合力矩为0.12Nm;
(2)当在秤钩上挂一物体时,将内套筒向右移动5cm,外套筒相对内套筒向右移动8cm,杆秤达到平衡,物体的质量为0.9kg.
(3)该物体实际质量为0.2kg.
则所求合力矩M=2mg(
| L |
| 2 |
(2)由力矩平衡得
m1gd=mgx1+mg(x1+x2)
解得m1=
| 2x1+x2 |
| d |
| 2×0.05+0.08 |
| 0.02 |
(3)正常称量1kg重物时,内外套筒可一起向外拉出x′
由力矩平衡得 m2′gd=2mgx′,x′=
| ||
| 2m |
外套筒丢失后,此时内套筒左端离称纽距离为x′-d=0.08m
由力矩平衡
m2gd+M=mg(x′-d+
| L |
| 2 |
解得m2=0.2kg
答:(1)当杆秤空载时,秤杆、配重物及挂钩所受重力相对秤纽的合力矩为0.12Nm;
(2)当在秤钩上挂一物体时,将内套筒向右移动5cm,外套筒相对内套筒向右移动8cm,杆秤达到平衡,物体的质量为0.9kg.
(3)该物体实际质量为0.2kg.
点评:本题考查理论联系实际,运用物理知识处理实际问题的能力.注意第(2)问中列式时,秤杆、配重物及挂钩所受重力相对秤纽的合力矩与两套筒的重力原来相对秤纽的力矩平衡,未列出.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目