Question

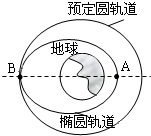“神舟六号”载人飞船于2005年10月12日上午9点整在酒泉航天发射场发射升空．由长征运载火箭将飞船送入近地点为A、远地点为B的椭圆轨道上，A点距地面的高度为h₁，飞船飞行五圈后进行变轨，进入预定圆轨道，如图所示．在预定圆轨道上飞行N圈所用时间为t，于10月17日凌晨在内蒙古草原成功返回．已知地球表面重力加速度为g，地球半径为R．求：
（1）飞船在A点的加速度大小．
（2）远地点B距地面的高度．
（3）沿着椭圆轨道从A到B的时间．

Answer 1

分析：（1）根据万有引力公式以及黄金代换式GM=gR²，求出飞船在A点所受的合力，从而求出加速度．
（2）根据万有引力提供向心力，G

Mm

r2

=mr(

2π

T

)2，已知周期，求出轨道半径，从而求出高度．
（3）根据开普勒第三定律

R3

T2

=C，求出椭圆轨道的周期．

解答：解：（1）飞船在A点所受的万有引力F=G

Mm

(R+h1)2

．
        由黄金代换式GM=gR²，得F=

gR2m

(R+h1)2

，
根据牛顿第二定律a=

F

m

=

gR2

(R+h1)2

．
故飞船在A点的加速度为

gR2

(R+h1)2

．
（2）G

Mm

r2

=mr(

2π

T

)2，T=

t

N

所以r=

3	GMt2 4π2N2

由黄金代换式GM=gR²，r=

3	gR2t2 4π2N2

，所以h=

3	gR2t2 4π2N2

-R
故远地点B距地面的高度为

3	gR2t2 4π2N2

-R．
（3）椭圆轨道的半长轴R′=

r+R+h1

2

=

3 gR2t2 4π2N2 +R+h1

2

根据开普勒第三定律

R′3

T′2

=

r3

T2

T′=

R′3T2 r3

=2π

( 3 gR2t2 4π2N2 +R+h1)3 8gR2

所以沿着椭圆轨道从A到B的时间t′=

T′

2

=π

( 3 gR2t2 4π2N2 +R+h1)3 8gR2

点评：解决本题的关键掌握黄金代换式GM=gR²，万有引力提供向心力，G

Mm

r2

=mr(

2π

T

)2，以及开普勒第三定律

R3

T2

=C．