题目内容
如图有一个竖直固定在地面的透气圆筒,筒中有一劲度系数为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料——ER流体,它对滑块的阻力可调。起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L,现有一质量为M=2m的物体从距地面2L处自由落下,与滑块瞬间碰撞后粘在一起向下运动。为保证滑块做匀减速运动,且下移距离为 (g为重力加速度)时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
(g为重力加速度)时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
(1)下落物体与滑块碰撞过程中系统损失的机械能;
(2)在滑块下移停止之前的过程中,ER流体对滑块阻力的大小f与下滑距离d所满足的函数关系式。
 (g为重力加速度)时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
(g为重力加速度)时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):(1)下落物体与滑块碰撞过程中系统损失的机械能;
(2)在滑块下移停止之前的过程中,ER流体对滑块阻力的大小f与下滑距离d所满足的函数关系式。

解:(1)设M与m碰撞前的速度大小为V1,由机械能守恒得:
MgL=MV12/2 ①
设碰撞后粘在一起的初速度大小为V2,由动量守恒定律得:
MV1=(M+m)V2 ②
在碰撞中损失的机械能为△E=MV12/2-(M+m)V22/2 ③
又M=2m ④
由①、②、③、④解得:△E=2mgL/3 ⑤
(2)相碰前弹簧的压缩量为x1=mg/k ⑥
共同下移到静止h=3mg/k ⑦
设加速度的大小为a,由匀变速直线运动公式有:
V22=2ah ⑧
设滑块下滑距离d时受到ER流体的阻力大小为f,此时弹簧的压缩量为x2,则
x2=x1+d ⑨
由牛顿第二定律得:f+kx2-(M+m)g=(M+m)a ⑩
由①、②、④、⑥、⑦、⑧、⑨、⑩得:f=2mg-kd+4kL/9
MgL=MV12/2 ①
设碰撞后粘在一起的初速度大小为V2,由动量守恒定律得:
MV1=(M+m)V2 ②
在碰撞中损失的机械能为△E=MV12/2-(M+m)V22/2 ③
又M=2m ④
由①、②、③、④解得:△E=2mgL/3 ⑤
(2)相碰前弹簧的压缩量为x1=mg/k ⑥
共同下移到静止h=3mg/k ⑦
设加速度的大小为a,由匀变速直线运动公式有:
V22=2ah ⑧
设滑块下滑距离d时受到ER流体的阻力大小为f,此时弹簧的压缩量为x2,则
x2=x1+d ⑨
由牛顿第二定律得:f+kx2-(M+m)g=(M+m)a ⑩
由①、②、④、⑥、⑦、⑧、⑨、⑩得:f=2mg-kd+4kL/9

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
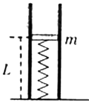 如图所示,图中有一个竖直固定在地面的透气圆筒,筒中有一劲度为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料--ER流体,它对滑块的阻力可调.起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现突然给滑块一个向下的大小为
如图所示,图中有一个竖直固定在地面的透气圆筒,筒中有一劲度为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料--ER流体,它对滑块的阻力可调.起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现突然给滑块一个向下的大小为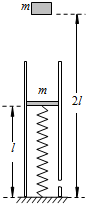 如图所示,有一个竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为f=
如图所示,有一个竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为f=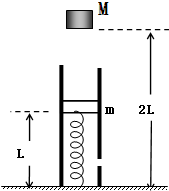 (2010?宿州二模)如图中有一个竖直固定在地面的透气圆筒,筒中有一劲度为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料-ER流体,它对滑块的阻力可调.起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L,现有一质量为M=2m的物体从距地面2L处自由落下,与滑块瞬间碰撞后粘在一起向下运动.为保证滑块做匀减速运动,且下移距离为
(2010?宿州二模)如图中有一个竖直固定在地面的透气圆筒,筒中有一劲度为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料-ER流体,它对滑块的阻力可调.起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L,现有一质量为M=2m的物体从距地面2L处自由落下,与滑块瞬间碰撞后粘在一起向下运动.为保证滑块做匀减速运动,且下移距离为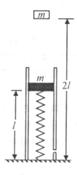 如图所示,有一个竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为
如图所示,有一个竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为