题目内容
9.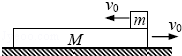 如图所示,在光滑水平面上,有一质量M=3kg的薄板,板上有质量m=1kg的物块,两者以v0=4m/s的初速度朝相反方向运动.薄板与物块间有摩擦且薄板足够长,运动过程中产生的内能全部由物块和薄板吸收且物块与薄板吸收的内能之比为2:1,求:
如图所示,在光滑水平面上,有一质量M=3kg的薄板,板上有质量m=1kg的物块,两者以v0=4m/s的初速度朝相反方向运动.薄板与物块间有摩擦且薄板足够长,运动过程中产生的内能全部由物块和薄板吸收且物块与薄板吸收的内能之比为2:1,求:①物块最后的速度;
②物块吸收的内能.
分析 ①物块与薄板运动的过程中,水平方向不受力,满足动量守恒定律,根据系统动量守恒列出等式求解物块的最终速度;
②整个的过程中,系统产生的内能等于相同损失的动能,由能量守恒列出等式求解产生的内能,再根据比例分开即可;
解答 解:①在摩擦力作用下物块和薄板最后共同运动,设共同运动速度为v,以向右为正方向,由动量守恒定律得:
Mv0-mv0=(M+m)v
代入数据解得:v=2 m/s,方向水平向右;
②在整个的过程中系统动能减少转化为摩擦产生的内能,由能量守恒得摩擦产生的内能:
Q=$\frac{1}{2}(M+m){v}_{0}^{2}-\frac{1}{2}(M+m){v}^{2}$
解得:Q=24J
物块与薄板吸收的内能之比为Q1:Q2=2:1
又:Q1+Q2=Q
所以:物块吸收的内能:${Q}_{1}=\frac{2}{3}Q=\frac{2}{3}×24=16$J
答:①物块最后的速度是2m/s;②物块吸收的内能是16J.
点评 本题考查了滑块在小车上滑动有关的动量、能量问题,掌握动量守恒和能量守恒结合求解问题的方法,熟悉不同形式的能量的相互转化,有一定综合性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.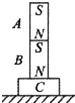 如图所示,条形磁铁A、B质量均为m,C为木块,它们放在水平面上静止时,B对A的弹力为F1,C对B的弹力为F2,则F1、F2与重力mg的大小关系正确的是( )
如图所示,条形磁铁A、B质量均为m,C为木块,它们放在水平面上静止时,B对A的弹力为F1,C对B的弹力为F2,则F1、F2与重力mg的大小关系正确的是( )
 如图所示,条形磁铁A、B质量均为m,C为木块,它们放在水平面上静止时,B对A的弹力为F1,C对B的弹力为F2,则F1、F2与重力mg的大小关系正确的是( )
如图所示,条形磁铁A、B质量均为m,C为木块,它们放在水平面上静止时,B对A的弹力为F1,C对B的弹力为F2,则F1、F2与重力mg的大小关系正确的是( )| A. | Fl=mg,F2=2mg | B. | F1>mg,F2=2mg | C. | Fl>mg,F2=mg | D. | F1=mg,F2>2mg |
17. 如图所示,甲物体从高H(H>1m)处自由下落,乙物体从高2H处自由下落,则关于他们的说法正确的是( )
如图所示,甲物体从高H(H>1m)处自由下落,乙物体从高2H处自由下落,则关于他们的说法正确的是( )
 如图所示,甲物体从高H(H>1m)处自由下落,乙物体从高2H处自由下落,则关于他们的说法正确的是( )
如图所示,甲物体从高H(H>1m)处自由下落,乙物体从高2H处自由下落,则关于他们的说法正确的是( )| A. | 下落1秒时甲物体速度大于乙物体速度 | |
| B. | 下落1米时甲物体速度等于乙物体速度 | |
| C. | 甲物体的加速度小于乙物体的加速度 | |
| D. | 两物体到达地面时的速度相同 |
14. 如图所示,一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动,杆最初处于水平位置,杆上距O为a=20cm处放有一小物体(可视为质点),杆与其上小物体最初均处于静止状态.若此杆突然以匀角速度ω绕O顺时针匀速转动.若小物体一定能与杆相碰,则角速度ω的取值范围有( )
如图所示,一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动,杆最初处于水平位置,杆上距O为a=20cm处放有一小物体(可视为质点),杆与其上小物体最初均处于静止状态.若此杆突然以匀角速度ω绕O顺时针匀速转动.若小物体一定能与杆相碰,则角速度ω的取值范围有( )
 如图所示,一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动,杆最初处于水平位置,杆上距O为a=20cm处放有一小物体(可视为质点),杆与其上小物体最初均处于静止状态.若此杆突然以匀角速度ω绕O顺时针匀速转动.若小物体一定能与杆相碰,则角速度ω的取值范围有( )
如图所示,一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动,杆最初处于水平位置,杆上距O为a=20cm处放有一小物体(可视为质点),杆与其上小物体最初均处于静止状态.若此杆突然以匀角速度ω绕O顺时针匀速转动.若小物体一定能与杆相碰,则角速度ω的取值范围有( )| A. | ω<$\frac{5}{4}$πrad/s | B. | ω<$\frac{5}{2}$πrad/s | ||
| C. | ω>$\frac{45}{4}$πrad/s | D. | ω≥$\frac{45}{8}$nπrad/s(n=1,2,3…) |

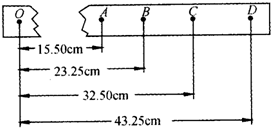 在“验证机械能守恒定律”的实验中:
在“验证机械能守恒定律”的实验中:
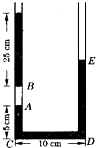 如图所示,截面均匀的U形玻璃细管两端都开口,玻璃管足够长,管内有两段水银柱封闭着一段空气柱,若气柱温度是27℃时,空气柱在U形管的左侧,A、B两点之间封闭着的空气柱长为15cm,U形管底边长CD=10cm,AC高为5cm.已知此时的大气压强为75cmHg.
如图所示,截面均匀的U形玻璃细管两端都开口,玻璃管足够长,管内有两段水银柱封闭着一段空气柱,若气柱温度是27℃时,空气柱在U形管的左侧,A、B两点之间封闭着的空气柱长为15cm,U形管底边长CD=10cm,AC高为5cm.已知此时的大气压强为75cmHg.