Question

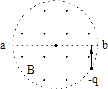
【题目】半径为R的固定半圆形玻璃砖的横截面如图所示，O点为圆心，OO′为直径MN的垂线．足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直．一束复色光沿半径方向与OO′成θ=30°角射向O点，已知复色光包含有折射率从n1= 到n2= 的光束，因而光屏上出现了彩色光带．
（ⅰ）求彩色光带的宽度；
（ⅱ）当复色光入射角逐渐增大时，光屏上的彩色光带将变成一个光点，求θ角至少为多少？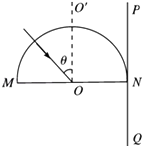

Answer 1

【答案】解：（ⅰ）由折射定律
n= ，n2=
代入数据，解得：
β1=45°，β2=60°
故彩色光带的宽度为：Rtan45°﹣Rtan30°=（1﹣ ）R
（ⅱ）当所有光线均发生全反射时，光屏上的光带消失，反射光束将在PN上形成一个光点．即此时折射率为n1的单色光在玻璃表面上恰好先发生全反射，故
sinC= =
即入射角θ=C=45°
答：（ⅰ）彩色光带的宽度为（1﹣ ）R；
（ⅱ）当复色光入射角逐渐增大时，光屏上的彩色光带将变成一个光点，θ角至少为45°
【解析】（1）根据折射定律求出折射角，几何关系求解两个光斑之间的距离；（2）为使光屏上的彩色光带消失，要使光线发生全反射．由于n1＜n2 ， 玻璃对其折射率为n2的色光先发生全反射，由临界角公式求解为使光屏上的彩带消失，复色光的入射角的最小值．
【考点精析】本题主要考查了光的折射的相关知识点，需要掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射才能正确解答此题．