Question

（2011?静安区二模）如图所示，质量m=1Kg的小球穿在长L=1.6m的斜杆上，斜杆与水平方向成α=37°角，斜杆固定不动，小球与斜杆间的动摩擦因数μ=0.75．小球受水平向左的拉力F=1N，从斜杆的顶端由静止开始下滑，求（sin37°=0.6，cos37°=0.8，g=10m/s²）
（1）小球运动的加速度大小；
（2）小球运动到斜杆底端时的速度大小．

Answer 1

分析：（1）对小球进行受力分析，求出合力，根据牛顿第二定律求出加速度．
（2）根据v²=2ax可求小球运动到斜杆底端时的速度大小．

解答：解：（1）小球受力分析如图所示

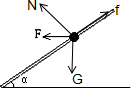
由牛顿第二定律得：Fcosα+mgsinα-μN=ma     ①
Fsinα+N=mgcosα        ②
①②联立得：a=

F(cosα+μsinα)+mg(sinα-μcosα)

m

=

1×(0.8+0.75×0.6)+10(0.6-0.75×0.8)

1

m/s2=1.25m/s²
（2）由公式v²=2ax得：
v=

2aL

=

2×1.25×1.6

=2m/s
答：（1）小球运动的加速度大小1.25m/s²；
（2）小球运动到斜杆底端时的速度大小2m/s．

点评：解题的关键是正确对小球进行受力分析，会用正交分解的方法求解合力，难度适中．