题目内容
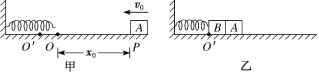
【题目】如图甲所示,轻弹簧左端固定在竖直墙上,右端点在O点位置。质量为m的物块A(可视为质点)以初速度v0从距O点右方x0的P点处向左运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与水平面间的动摩擦因数为μ,重力加速度为g,不计空气阻力。
(1)物块A从O点O′点O点的过程,弹簧弹力所做的功W弹;
(2)求物块A从P点出发又回到P点的全过程,摩擦力所做的功Wf;
(3)如图乙所示,若将另一个物块B(可视为质点)与弹簧右端拴接,B与地面间的动摩擦因数也为μ,将A放在B右边,向左缓慢推A,使弹簧右端压缩到O′点位置,然后从静止释放,若B的质量M在“合适”的范围内取不同的值,A、B都可以共同滑行一段距离后分离。若M在“合适”的范围内取值变大,A、B的分离位置会变化吗?给出结论并论证。
【答案】(1)0(2) -![]() mv02 (3) 与M无关
mv02 (3) 与M无关
【解析】
(1) 弹簧初 末位置相同,弹簧弹力做功为 0
(2)物块A从P点出发又回到P点的过程,根据动能定理得
W支+ WG+W弹+Wf=0-![]() mv02
mv02
其中,W支=WG=W弹=0。
故
Wf=-![]() mv02(无负号不得分)
mv02(无负号不得分)
(3) A、B的分离位置不会变化。论证:设A、B分离时弹簧的处于压缩状态,压缩量为x,则分离时刻,A、B两物体在受力和运动上具有如下特征:受力上,A、B间的弹力为0,运动上,A、B的加速度相同,即
aA=aB①
(隔离法)分别分析A、B的受力,以向右为正方向,
对A根据牛顿第二定律有
aA=![]() ②
②
对B根据牛顿第二定律有
aB=![]() ③
③
由①②③可得x=0,这意味着A、B分离时弹簧处于原长,这一结论与M无关(只要M在“合适”的范围内取值)。

练习册系列答案
相关题目