题目内容
【题目】如图所示,倾角θ=37°的倾斜轨道和水平轨道平滑连接且固定不动,小物块与两轨道间的动摩擦因数均为μ=0.5,小物块从斜面上A点静止释放,最终停止在水平轨道上的B点,已知小物块从释放至停止滑行的总路程s=1.4m.sin37°=0.6,cos37°=0.8,g=10m/s2 . 求: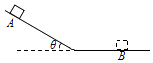
(1)小物块运动过程中的最大速度vm;
(2)静止释放小物块后1.2s内的平均速率.
【答案】
(1)解:小物块在倾斜轨道上匀加速下滑,由牛顿第二定律得:
mgsinθ﹣μmgcosθ=ma1.
代入数据解得 a1=2m/s2.
小物块在水平轨道上匀减速滑行,由牛顿第二定律得:
μmg=ma2.
代入数据解得:a2=2m/s2.
由运动学公式得:s= ![]() +
+ ![]()
代入数据解得:vm=2m/s
答:小物块运动过程中的最大速度vm是2m/s.
(2)解:小物块在倾斜轨道上运动时间为:t1= ![]() =
= ![]() =1s
=1s
路程为:s1= ![]() =
= ![]() m=1m
m=1m
到t1时刻小物块在水平轨道上运动的路程为:
s2=vm(t﹣t1)﹣ ![]()
代入数据解得:s2=0.3m
所以静止释放小物块后1.2s内的平均速率为:
![]() =
= ![]() =
= ![]() =
= ![]() m/s
m/s
答:静止释放小物块后1.2s内的平均速率是 ![]() m/s.
m/s.
【解析】(1)根据牛顿第二定律求出小物块在斜面上和水平面上运动的加速度大小,再对两个过程,分别运用速度位移公式列式,即可求解最大速度.(2)平均速率等于路程与时间之比.根据运动学公式分别求两个过程的时间和位移大小,再求平均速率.
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系的相关知识点,需要掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值才能正确解答此题.