题目内容
【题目】设有一湖水足够深的咸水湖,湖面宽阔而平静.初始时将一体积很小的匀质正立方体物块在湖面上由静止开始释放,释放时物块的下底面和湖水表面恰好相接触.已知湖水密度为![]() ;物块边长为b,密度为
;物块边长为b,密度为![]() ,且
,且![]() .在只考虑物块受重力和液体浮力作用的情况下,求物块从初始位置出发往返一次所需的时间.
.在只考虑物块受重力和液体浮力作用的情况下,求物块从初始位置出发往返一次所需的时间.
【答案】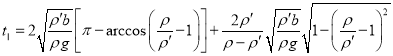
【解析】
由于湖面足够宽阔而物块体积很小,湖面的绝对高度在物块运动过程中始终保持不变,因此,可选湖面为坐标原点并以竖直向下方向为正方向建立坐标系,以下简称x系.设物块下底面的坐标为x,在物块未完全浸没入湖水时,其所受到的浮力为
![]() , ①
, ①
式中g为重力加速度。
物块的重力为![]() . ②
. ②
设物块的加速度为a,根据牛顿第二定律有
![]() ③
③
将①和②式代入③式得![]() . ④
. ④
将x系坐标原点向下移动![]() 而建立新坐标系,简称X系.新旧坐标的关系为
而建立新坐标系,简称X系.新旧坐标的关系为
![]() . ⑤
. ⑤
把⑤式代入④式得![]() . ⑥
. ⑥
⑥式表示物块的运动是简谐振动.若X=0,则a=0,对应于物块的平衡位置.由⑤式可知,当物块处于平衡位置时,物块下底面在x系中的坐标为
![]() ⑦
⑦
物块运动方程在X系中可写为
![]() ⑧
⑧
利用参考圆可将其振动速度表示为
![]() , ⑨
, ⑨
式中![]() 为振动的圆频率,
为振动的圆频率,![]() ⑩
⑩
在⑧和⑨式中A和![]() 分别是振幅和初相位,由初始条件决定.在物块刚被释放时,即t=0时刻有x=0,由⑤式得
分别是振幅和初相位,由初始条件决定.在物块刚被释放时,即t=0时刻有x=0,由⑤式得
![]() ,
,
![]() .
.
由⑧至式可求得![]()
![]() .
.
将⑩和式分别代入⑧和⑨式得
![]() ,
,
![]()
由式可知,物块再次返回到初始位置时恰好完成一个振动周期.但物块的运动始终由表示是有条件的,那就是在运动过程中物块始终没有完全浸没在湖水中.若物块从某时刻起全部浸没在湖水中,则湖水作用于物块的浮力变成恒力,物块此后的运动将不再是简谐振动,物块再次返回到初始位置所需的时间也就不再全由振动的周期决定。为此,必须研究物块可能完全浸没在湖水中的情况。显然,在x系中看,物下底面坐标为b时,物块刚好被完全浸没.由⑤式知在X系中这一临界坐标值为
![]()
即物块刚好完全浸没在湖水中时,其下底面在平衡位置以下![]() 处.注意到在振动过程中,物块下底面离平衡位置的最大距离等于振动的振幅A.下面分两种情况讨论,
处.注意到在振动过程中,物块下底面离平衡位置的最大距离等于振动的振幅A.下面分两种情况讨论,
Ⅰ.![]() ,由和两式得
,由和两式得![]() .
.
在这种情况下,物块在运动过程中至多刚好全部浸没在湖水中.因而,物块从初始位置起,经一个振动周期,再次返回至初始位置.由⑩式得振动周期为
![]()
物块从初始位置出发往返一次所需的时间为
![]()
Ⅱ.![]() ,由和两式得
,由和两式得![]() .
.
在这种情况下,物块在运动过程中会从某时刻起全部浸没在湖水表面之下.设从初始位置起,经过时间![]() 物块刚好全部浸入湖水中,这时
物块刚好全部浸入湖水中,这时![]() .由和式得
.由和式得
![]()
取合理值,有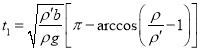
由上式和式可求得这时物块的速度为
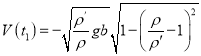
此后,物块在液体内作匀减速运动,以![]() 表示加速度的大小,由牛顿定律有
表示加速度的大小,由牛顿定律有
![]()
设物块从刚好完全浸入湖水到速度为零时所用的时间为![]()
由![]()
得
物块从初始位置出发往返一次所需的时间为