Question

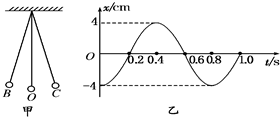如图甲所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙所示是这个单摆的振动图象．根据图象回答：（π²=10）
（1）单摆振动的频率是多大？
（2）若当地的重力加速度为10m/s²，试求这个摆的摆长是多少？
（3）如果摆球在B处绳上拉力F₁=0.995N，在O处绳上拉力F₂=1.01N，则摆球质量是多少？

Answer 1

分析：（1）单摆做简谐运动，完成一次全振动的时间为一个周期，图上相邻两个最大值之间的时间间隔为一个周期．由图象求出单摆的周期，然后求出频率．
（2）已知单摆周期与当地的重力加速度，由单摆周期公式的变形公式可以求出摆长．
（3）B处绳子的拉力等于重力的切向分力，O处绳子的张力和重力的合力提供向心力，根据牛顿第二定律和机械能守恒定律列式求解即可．

解答：解：（1）由图乙可知：T=0.8 s       
则f=

1

T

=1.25 Hz  
（2）由T=2π

l g

，得：l=

gT2

4π2

=

10×0．82

4×10

=0.16 m．
（3）在B点，沿绳子方向平衡，有：
F_A=mgcosα
在0点有：
FB-mg=m

v2

L

从B点到O点根据机械能守恒有：
mgL(1-cosα)=

1

2

mv2
联立可得摆球质量：m=0.1kg
答：（1）单摆振动的频率是1.25Hz；
（2）这个摆的摆长是0.16m；
（3）摆球质量是0.1kg．

点评：本题关键是明确摆球的运动学规律和动力学规律，然后结合牛顿第二定律和机械能守恒定律列式分析，不难．