题目内容
如图2-3-17所示,将一根不能伸长的柔软轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F1;将绳子B端移到C点,保持整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子B端移到D点时,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,则( )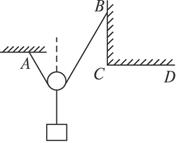
图2-3-17
A.θ1=θ2=θ3 B.θ1=θ2<θ3
C.F1>F2>F3 D.F1=F2<F1
思路点拨:本题考查三个共点力作用下的动态平衡,动态平衡问题是指通过控制某些物理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态中.这道题是关于绳子的一个典型问题,同一轻绳上张力处处相等的特点是这类题目的一个重要隐含条件,受力分析后建立平面直角坐标系,得出各力的关系,然后加以讨论.
解析:设绳长为l,A、B两点间的水平距离为d,竖直悬绳与滑轮两侧两软绳间的夹角为θ/2.绳子B端从B移到C,sin![]() =
=![]() 没有发生变化,所以θ1=θ2=θ.在D点有sin
没有发生变化,所以θ1=θ2=θ.在D点有sin![]() =
=![]() ,d′为绳两端点间的水平距离,因d′>d,所以θ′>θ,所以选项B正确.因θ1=θ2,所以绳中拉力F=
,d′为绳两端点间的水平距离,因d′>d,所以θ′>θ,所以选项B正确.因θ1=θ2,所以绳中拉力F= 是相等的,即F1=F2.而θ3>θ2,所以绳中拉力有F3>F2,所以选项D正确.故BD正确.
是相等的,即F1=F2.而θ3>θ2,所以绳中拉力有F3>F2,所以选项D正确.故BD正确.
答案:BD

练习册系列答案
相关题目