题目内容
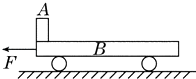
【题目】如图所示，在光滑的水平面上停放着小车B，车上左端有一可视为质点的小物块A，A和B之间的接触面前一段光滑，后一段粗糙，且后一段的动摩擦因数μ=0.4，小车长L=2m，A的质量 mA=1kg，B的质量mB=4kg，现用12N的水平力F向左拉动小车，当A到达B的最右端时，两者速度恰好相等，求：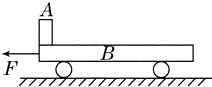
（1）A在B的光滑和粗糙部分运动时，两个物体的加速度；
（2）A和B间光滑部分的长度．（g取10m/s2）
【答案】
（1）解：A在B的光滑部分运动时
aA1=0 aB1= 
=3m/s2
A在B的粗糙部分运动时
aA2=μg=4 m/s2 aB2= 
=2m/s2
答：两个物体的加速度分别为4m/s2、2m/s2
（2）解：设小车B光滑部分的长度x1，小车B此过程中运动时间为t1，
v1=aB1t1 x1= 
aB1t 
当A进入到小车B的粗糙部分后，两者达到相同的速度经历的时间为t2，且共同速度则有：
v1+aB2t2=aA2t2
v1t2+ aB2t 
﹣ aA2t =L﹣x1，
综合以上各式并代入数据可得A和B间光滑部分的长度：x1=0.8 m
答：A和B间光滑部分的长度为0.8m
【解析】（1）根据牛顿第二定律分别求出A在B的光滑和粗糙部分运动时两个物体的加速度．（2）在光滑部分，A静止，B做匀加速直线运动，在粗糙部分，A做匀加速直线运动，B做匀加速直线运动，结合到达最右端的速度相等，结合速度关系和位移关系运用运动学公式求出光滑部分的长度．
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值．
【题目】甲乙两同学做测定木板与铁块之间的动摩擦因数的实验时，设计了甲乙两种方案：
方案甲：木板固定，用弹簧秤拉动铁块，如图甲所示；
方案乙：铁块通过弹簧秤与墙连接，用手拉动木板，如图乙所示．
实验器材有：弹簧秤、木板、质量为400g的铁块、细线、质量为200g的配重若干．（g=10m/s2）
①上述两种方案你认为更合理的方案是______（填“甲”或“乙”）
②某同学在铁块上加上配重，改变铁块对木板的正压力，记录了实验数据如下表所示：
实验次数 | 1 | 2 | 3 | 4 | 5 |
配重（个数） | 0 | 1 | 2 | 3 | 4 |
弹簧秤读数/N | 1.00 | 1.50 | 2.00 | 2.20 | 3.00 |
请根据上述数据在图丙中画出铁块所受摩擦力Ff和压力FN的关系图象；由图象可求出木板和铁块间动摩擦因数是__________
