Question

【题目】某人骑电动自行车经过如图甲所示的铁路涵洞，图乙是其道路示意图，倾斜道路 AB、 CD 与水平道路 BC 的夹角均为 30°，AD 与 BC 的高度差为 2.5m。当他从 A 点下行时，为了避免因速度过大而造成危险，他适当用力握住手刹，使其所受阻力为人和车总重力的 0.25 倍。已 知人和车的总质量为 m=100kg，在 A 点时行驶速度很小（可视为零），行驶在 CD 段时受到的阻 力恒为其重力的 0.1 倍。求：

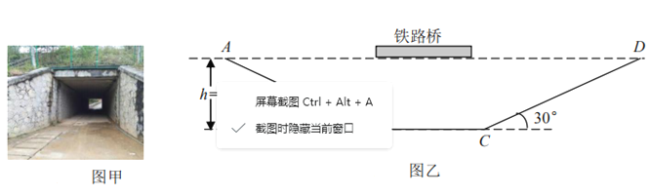
（1）车在 AB 段下行的加速度大小 a1；

（2）车到达 B 点时的速度大小 vB；

（3）欲使车沿 CD上行而不会减速，电动机工作使车受到的最小牵引力大小 Fmin。

Answer 1

【答案】（1）2.5m/s2（2） 5m/s（3）600N

【解析】

运用牛顿第二定律列式求解加速度；根据运动学公式求解速率，要沿CD上行而不停下来，必须满足F≥mgsin30°+f2。

（1）根据牛顿第二定律：mgsin30°-f1=ma1 其中：f1=0.25mg

解得：a1= 2.5m/s2

（2） A→B过程做匀加速直线运动

运动的距离为：LAB=

由速度位移公式：

解得：vB=5m/s

（3）要沿CD上行而不停下来，必须满足F≥mgsin30°+f2

代入数据可得：Fmin=mgsin30°+f2= 600N