题目内容
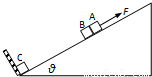
如图所示,可视为质点的三物块A、B、C放在倾角为θ=30°、长为L=2m的固定斜面上,三物块与斜面间的动摩擦因数均为μ=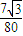 ,A与B紧靠在一起,C紧靠在固定挡板上,其中A为不带电的绝缘体,B、C所带电荷量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,A、B的质量分别为mA=0.80kg、mB=0.64kg.开始时三个物块均能保持静止状态,且此时A、B两物体与斜面间恰无摩擦力作用.如果选定两点电荷在相距无穷远处的电势能为零,则相距为r时,两点电荷具有的电势能可表示为EP=k
,A与B紧靠在一起,C紧靠在固定挡板上,其中A为不带电的绝缘体,B、C所带电荷量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,A、B的质量分别为mA=0.80kg、mB=0.64kg.开始时三个物块均能保持静止状态,且此时A、B两物体与斜面间恰无摩擦力作用.如果选定两点电荷在相距无穷远处的电势能为零,则相距为r时,两点电荷具有的电势能可表示为EP=k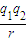 .为使A在斜面上始终做加速度为a=1.5m/s2的匀加速直线运动,现给A施加一平行于斜面向上的力F,已知经过时间t后,力F的大小不再发生变化.当A运动到斜面顶端时,撤去外力F.求:
.为使A在斜面上始终做加速度为a=1.5m/s2的匀加速直线运动,现给A施加一平行于斜面向上的力F,已知经过时间t后,力F的大小不再发生变化.当A运动到斜面顶端时,撤去外力F.求:(1)未施加力F时物块B、C间的距离;
(2)t时间内A上滑的距离;
(3)t时间内库仑力做的功;
(4)在A由静止开始到运动至斜面顶端的过程中,力F对A做的总功.
【答案】分析:(1)未施加力F时,A、B处于静止状态,合力为零,根据平衡条件和库仑定律求解物块B、C间的距离.
(2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小,经过时间t物体A、B分离时,它们之间的弹力变为零,根据牛顿第二定律和库仑定律结合可求出t时间内A上滑的距离.
(3)t时间内库仑力做的功等于B的电势能的变化,根据功能关系求解.
(4)对系统运用动能定理,求出变力F对物体做功;再由牛顿第二定律与功的表达式,求出恒力F对物体做的功,最后两者之和即为力F对物块A做的总功.
解答:解:(1)未施加力F时,A、B、C处于静止状态时,设B、C间距离为L1,则 C对B的库仑斥力:
F=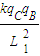
以A、B为研究对象,根据力的平衡:F=(mA+mB)gsin30°
联立解得:L1=1.0m
(2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小.经过时间t,B、C间距离设为L2,A、B两者间弹力减小到零,此后两者分离,力F变为恒力.则t时刻C对B的库仑斥力为:F1=k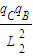 …①
…①
以B为研究对象,由牛顿第二定律有:
F1-mBgsin30°-μmBgcos30°=mBa…②
联立①②解得:L2=1.2m
则t时间内A上滑的距离:△L=L2-L1=0.2m
(3)设t时间内库仑力做的功为W,由功能关系有:
W=k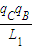 -k
-k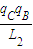 代入数据解得:W=1.2J…③
代入数据解得:W=1.2J…③
(4)设在t时间内,末速度为v1,力F对A物块做的功为W1,由动能定理有:
W1+W+WG+Wf= (mA+mB)
(mA+mB)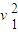 …④
…④
而 WG=-(mA+mB)g?△Lsin30°…⑤
Wf=-μ(mA+mB)g?△Lcos30°…⑥
又A做匀加速运动,则有: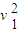 =2a△L…⑦
=2a△L…⑦
由③~⑦式解得:E1=1.05J
经过时间t后,A、B分离,力F变为恒力,对A由牛顿第二定律有:
F-mAgsin30°-μmAgcos30°=mAa…⑧
力F对A物块做的功:W2=F(L-L2)…⑨
由⑧⑨式代入数据得:W2=5J
则力F对A物块做的功:W=W1+W2=6.05J
答:
(1)未施加力F时物块B、C间的距离为1m:
(2)t时间内A上滑的距离是0.2m;
(3)t时间内库仑力做的功是1.2J;
(4)力F对A物块做的总功为6.05J.
点评:本题的设计属于陈题翻新.本题与含有弹簧的问题类似,用电势能代替弹性势能,保留重力的分立代替原重力.考查功能很直接:一是考查学生能否用熟悉的方法解决相似问题的能力,二是能否综合应用几乎全部力学规律(匀变速运动、牛顿第二定律、能量守恒定律)解决问题,不失为一道立意鲜明难度适当的好的综合题.
(2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小,经过时间t物体A、B分离时,它们之间的弹力变为零,根据牛顿第二定律和库仑定律结合可求出t时间内A上滑的距离.
(3)t时间内库仑力做的功等于B的电势能的变化,根据功能关系求解.
(4)对系统运用动能定理,求出变力F对物体做功;再由牛顿第二定律与功的表达式,求出恒力F对物体做的功,最后两者之和即为力F对物块A做的总功.
解答:解:(1)未施加力F时,A、B、C处于静止状态时,设B、C间距离为L1,则 C对B的库仑斥力:
F=
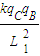
以A、B为研究对象,根据力的平衡:F=(mA+mB)gsin30°
联立解得:L1=1.0m
(2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小.经过时间t,B、C间距离设为L2,A、B两者间弹力减小到零,此后两者分离,力F变为恒力.则t时刻C对B的库仑斥力为:F1=k
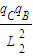 …①
…①以B为研究对象,由牛顿第二定律有:
F1-mBgsin30°-μmBgcos30°=mBa…②
联立①②解得:L2=1.2m
则t时间内A上滑的距离:△L=L2-L1=0.2m
(3)设t时间内库仑力做的功为W,由功能关系有:
W=k
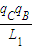 -k
-k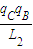 代入数据解得:W=1.2J…③
代入数据解得:W=1.2J…③(4)设在t时间内,末速度为v1,力F对A物块做的功为W1,由动能定理有:
W1+W+WG+Wf=
 (mA+mB)
(mA+mB)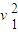 …④
…④而 WG=-(mA+mB)g?△Lsin30°…⑤
Wf=-μ(mA+mB)g?△Lcos30°…⑥
又A做匀加速运动,则有:
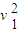 =2a△L…⑦
=2a△L…⑦由③~⑦式解得:E1=1.05J
经过时间t后,A、B分离,力F变为恒力,对A由牛顿第二定律有:
F-mAgsin30°-μmAgcos30°=mAa…⑧
力F对A物块做的功:W2=F(L-L2)…⑨
由⑧⑨式代入数据得:W2=5J
则力F对A物块做的功:W=W1+W2=6.05J
答:
(1)未施加力F时物块B、C间的距离为1m:
(2)t时间内A上滑的距离是0.2m;
(3)t时间内库仑力做的功是1.2J;
(4)力F对A物块做的总功为6.05J.
点评:本题的设计属于陈题翻新.本题与含有弹簧的问题类似,用电势能代替弹性势能,保留重力的分立代替原重力.考查功能很直接:一是考查学生能否用熟悉的方法解决相似问题的能力,二是能否综合应用几乎全部力学规律(匀变速运动、牛顿第二定律、能量守恒定律)解决问题,不失为一道立意鲜明难度适当的好的综合题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( ) (2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、
(2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、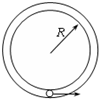 如图所示,可视为质点、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( ) 如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( )
如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( ) (1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是
(1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是