题目内容
如图所示,无重力空间中有一恒定的匀强磁场,磁感应强度的方向垂直于xoy平面向外,大小为B,沿x轴放置一个垂直于xoy平面的较大的荧光屏,P点位于荧光屏上,在y轴上的A点放置一放射源,可以不断地以平面内的不同方向以大小不等的速度放射出质量为m,电荷量为+q的同种粒子,这些粒子打到荧光屏上,能在屏上形成一条亮线,P点处在亮线上,已知OA=OP=L.

求:
(1)若能打到P点,则粒子速度的最小值为多少?
(2)若能打到P点,则粒子在磁场中运动的最长时间为多少?

求:
(1)若能打到P点,则粒子速度的最小值为多少?
(2)若能打到P点,则粒子在磁场中运动的最长时间为多少?
(1)v=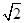 qBL/2m;(2)t=
qBL/2m;(2)t=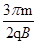
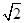 qBL/2m;(2)t=
qBL/2m;(2)t=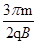
试题分析: (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,若粒子速度最小,则做圆周运动的半径最小,而AP连线必为圆周运动的一条弦,故以AP连线为直径时,对应粒子的最小速度
由牛顿第二定律 qvB=mv2/R (2分)
由几何关系 R=
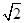 L/2 (2分)
L/2 (2分)得粒子的最小速度为 v=
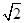 qBL/2m (2分)
qBL/2m (2分)(2)粒子在磁场中运动的周期
得T=2
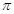 R /V (2分)
R /V (2分)当粒子在磁场中做3/4圆周时运动时间最长 (2分)
得t=
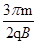 (2分)
(2分)
练习册系列答案
相关题目
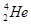 ,带电粒子在轨迹圆上运动的周期之比
,带电粒子在轨迹圆上运动的周期之比 。设衰变过程释放的核能全部转化成射线粒子和反冲核的动能,已知该衰变过程前后原子核的质量亏损为m。
。设衰变过程释放的核能全部转化成射线粒子和反冲核的动能,已知该衰变过程前后原子核的质量亏损为m。 ”或“
”或“ ”)
”)



 角斜向上射人磁场(此为第一次),且在上方运动半径为R(不计重力)。则( )
角斜向上射人磁场(此为第一次),且在上方运动半径为R(不计重力)。则( )
 轴上方和下方两磁场中运动的半径之比为2:1
轴上方和下方两磁场中运动的半径之比为2:1