题目内容
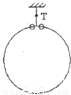
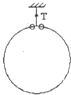 质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:
质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:(1)在圆环不动的条件下,悬线中的张力T随cosθ(θ为小珠和大环圆心连线与竖直方向的夹角)变化的函数关系,并求出张力T的极小值及相应的cosθ值;
(2)小珠与圆环的质量比
| m | M |
分析:(1)对其中任一小珠研究,根据机械能守恒求得速度与θ的关系式,小珠做圆周运动,指向圆心的合力提供向心力,根据牛顿第二定律求出小珠所受的圆环的弹力,再根据牛顿第三定律得到小珠对圆环的弹力,圆环处于静止状态,由平衡条件求出T与θ的关系式,再根据数学知识分析极小值及相应的cosθ值;
(2)当圆环所受的合力向上时,有可能上升,根据上问的结果进行讨论.
(2)当圆环所受的合力向上时,有可能上升,根据上问的结果进行讨论.
解答:解:(1)设小珠和大环圆心连线与竖直方向的夹角为θ时小珠的速度大小为v.
根据机械能守恒定律得:
mv2=mgR(1-cosθ)
设圆环对小珠的弹力大小为N,由牛顿第二定律得
mgcosθ-N=m
对于圆环,合力为零,则有
T=Mg+2Ncosθ
联立以上三式得:Ncosθ=6mgcos2θ-4mgcosθ,T=Mg+6mgcos2θ-4mgcosθ
根据抛物线方程知,当cosθ=-
=-
=
时,T有极小值,极小值为Tmin=Mg-
mg
(2)由上知,Tmin=Mg-
mg,说明此时小珠对圆环的作用力的合力方向向上,大小为N′=
mg
当N′>Mg时,圆环将会上升,则有Tmin=Mg-
mg<0
解得,
>
答:(1)在圆环不动的条件下,悬线中的张力T随cosθ变化的函数关系是T=Mg+6mgcos2θ-4mgcosθ,张力T的极小值是Mg-
mg,相应的cosθ值是
;
(2)小珠与圆环的质量比
至少为
时圆环才有可能上升.
根据机械能守恒定律得:
| 1 |
| 2 |
设圆环对小珠的弹力大小为N,由牛顿第二定律得
mgcosθ-N=m
| v2 |
| R |
对于圆环,合力为零,则有
T=Mg+2Ncosθ
联立以上三式得:Ncosθ=6mgcos2θ-4mgcosθ,T=Mg+6mgcos2θ-4mgcosθ
根据抛物线方程知,当cosθ=-
| b |
| 2a |
| -4mg |
| 12mg |
| 1 |
| 3 |
| 2 |
| 3 |
(2)由上知,Tmin=Mg-
| 2 |
| 3 |
| 2 |
| 3 |
当N′>Mg时,圆环将会上升,则有Tmin=Mg-
| 2 |
| 3 |
解得,
| m |
| M |
| 3 |
| 2 |
答:(1)在圆环不动的条件下,悬线中的张力T随cosθ变化的函数关系是T=Mg+6mgcos2θ-4mgcosθ,张力T的极小值是Mg-
| 2 |
| 3 |
| 1 |
| 3 |
(2)小珠与圆环的质量比
| m |
| M |
| 2 |
| 3 |
点评:本题运用机械能守恒、圆周运动、力平衡条件结合推导出T的表达式,再根据数学知识求解T的极小值.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
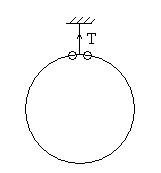 质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:
质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:
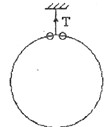
 (
(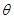 为小珠和大环圆心连线与竖直方向的夹角)变化的函数关系,并求出张力T的极小值及相应的
为小珠和大环圆心连线与竖直方向的夹角)变化的函数关系,并求出张力T的极小值及相应的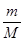 至少为多大时圆环才有可能上升?
至少为多大时圆环才有可能上升? 至少为多大时圆环才有可能上升?
至少为多大时圆环才有可能上升?