题目内容
7. 光滑水平面上有一质量为M=2kg的足够长的木板,木板上最有右端有一大小可忽略、质量为m=3kg的物块,物块与木板间的动摩擦因数μ=0.4,且最大静摩擦力等于滑动摩擦力.开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P.现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,求:
光滑水平面上有一质量为M=2kg的足够长的木板,木板上最有右端有一大小可忽略、质量为m=3kg的物块,物块与木板间的动摩擦因数μ=0.4,且最大静摩擦力等于滑动摩擦力.开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P.现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,求:(1)木板第一次撞击挡板P时的速度v为多少?
(2)木板从第一次撞击挡板P到运动至右端最远处所需的时间t1及此时物块距木板右端的距离x为多少?
(3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动.每次木板与挡板P撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板最右端的距离x为多少?
分析 (1)木板受最大静摩擦力产生的加速度和以整体为研究对象在拉力F作用下产生的加速度比较,确定木板做匀加速运动的加速度,然后根据速度位移关系求物体到达P点时的速度;
(2)分析木板的受力,根据牛顿第二定律,求木板匀减速运动的加速度,再根据速度时间关系求木板运动的时间,再根据时间求位移;
(3)在全过程中只有拉力和木板与物块的摩擦力做功,根据动能定理求出物块相对于木板时的位移.
解答 解:(1)设木板靠最大静摩擦力或滑动摩擦力产生的加速度为am,则:
am=$\frac{μmg}{M}$=6m/s2
若木板与物块不发生相对运动,设共同加速度为a1,则:
a1=$\frac{F}{M+m}$=1.2m/s2
因a1<am,所以木板与物块靠静摩擦力一起以加速度a1运动
根据匀变速直线运动的速度位移关系:v2=2a1L
解得木板第一次撞击挡板P时的速度:v=2.4m/s
(2)设木板第一次撞击挡板P后向右运动时,物块的加速度大小为a2,根据牛顿第二定律有:
μmg-F=ma2
解得物块的加速度:a2=2m/s2
因a2<am,所以在木板向右减速运动过程中,物块一直向左减速,木板速度减为0时,木块仍在向左运动.设木板第一次撞击挡板P后运动到右端最远处所需时间为t1,则:
t1=$\frac{v}{a_m}$=0.4s
设木板左端距挡板P的距离为X1,则:${X_1}=\frac{v^2}{{2{a_m}}}=0.48$m
设物块相对地向左的位移为X2,则:X2=vt1-$\frac{1}{2}$a2t12=0.8m
此时物块距木板右端的距离为:X=X1+X2=1.28m
(3)木板最终静止于挡板P处,设物块距木板右端的距离为Xn,此过程中只有拉力和摩擦力做功,根据动能定理有:F(Xn+L)-μmgXn=0
解得:Xn=2.4m
答:(1)木板第一次撞击挡板P时的速度v为多少2.4m/s;
(2)木板从第一次撞击挡板P到运动至有端最远处所需的时间t1及此时物块距木板右端的距离X为多少1.28m;
(3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动.每次木板与挡板p撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板有端的距离X为2.4m.
点评 处理本题的关键是用隔离法对物块和木板进行受力分析,由牛顿第二定律求出各自的加速度,再运用运动学规律求解.正确的受力分析和做功分析是解决本题的关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 物体的加速度大小为12m/s2 | B. | 物体的初速度大小为18m/s | ||
| C. | 物体速度为零的时刻1.5s | D. | 物体速度为零的时刻3s |
 如图所示,保持弹簧测力计1的度数不变,仅改变它的拉力方向,使角α减小.要使橡皮绳下端仍被拉到O点,可使( )
如图所示,保持弹簧测力计1的度数不变,仅改变它的拉力方向,使角α减小.要使橡皮绳下端仍被拉到O点,可使( )
| A. | 弹簧测力计2的读数增大,∠β减小 | B. | 弹簧测力计2的读数减小,∠β增大 | ||
| C. | 弹簧测力计2的读数增大,∠β增大 | D. | 弹簧测力计2的读数不变,∠β减小 |
| A. | 利用打点计时器在“研究匀变速直线运动规律”的实验中,可以根据纸带上的点迹计算物体的平均速度 | |
| B. | 在“验证力的平行四边形定则”实验中,要使力的作用效果相同,只需橡皮条具有相同的伸长量 | |
| C. | 在“验证牛顿第二定律”的实验中,需要先平衡摩擦力 | |
| D. | 在“验证机械能守恒定律”的实验中,应该先释放重物后接通电源 |
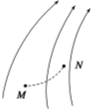 某静电场中的电场线为图示实线,带电粒子仅受电场力作用由M点运动到N点,其运动轨迹如图中虚线所示,以下说法正确的是( )
某静电场中的电场线为图示实线,带电粒子仅受电场力作用由M点运动到N点,其运动轨迹如图中虚线所示,以下说法正确的是( )| A. | 粒子带正电荷 | |
| B. | 由于M点没有电场线,粒子在M点不受电场力的作用 | |
| C. | 粒子在M点的加速度小于它在N点的加速度 | |
| D. | 粒子在M点的动能小于在N点的动能 |
 如图所示,一个质量为m、电荷量为q的粒子,从小孔S1飘入加速电场,其初速度可视为零,然后经点S3沿着与磁场垂直的方向进入磁感应强度为B的有界匀强磁场中,粒子恰能从磁场左边界的点S4射出,已知点S3、S4间距为L(不计粒子重力).求:
如图所示,一个质量为m、电荷量为q的粒子,从小孔S1飘入加速电场,其初速度可视为零,然后经点S3沿着与磁场垂直的方向进入磁感应强度为B的有界匀强磁场中,粒子恰能从磁场左边界的点S4射出,已知点S3、S4间距为L(不计粒子重力).求:

 在用打点计时器验证机械能守恒定律的实验中,质量m=1.00㎏的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么:
在用打点计时器验证机械能守恒定律的实验中,质量m=1.00㎏的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么: