��Ŀ����
6�������й�����ѧʷ������ѧ������˵���У�����ȷ���У�������| A�� | ٤�����о����������˶�ʱ��������������ʱ��̫�̣����ײ�������˲����ˡ��嵭�������ķ���������ʱ�䣬Ȼ���ٰѵó��Ľ��ۺ������� | |
| B�� | �����ٶȶ���ʽv=$\frac{��x}{��t}$������t�dz��dz�Сʱ��$\frac{��x}{��t}$�Ϳ��Ա�ʾ������tʱ�̵�˲ʱ�ٶȣ��ö���Ӧ���˼���˼�뷽�� | |
| C�� | ��a=$\frac{��v}{��t}$��֪������ļ��ٶ��ֽ����ٶȵı仯�ʣ���ֵ�ɱ�ֵ$\frac{��v}{��t}$���� | |
| D�� | ���Ƶ��ȱ����˶�λ�ƹ�ʽʱ���������˶����̻��ֳɺܶ�С�Σ�ÿһС�ν��ƿ�������ֱ���˶���Ȼ��Ѹ�С�ε�λ����ӣ����������Ԫ�� |
���� �ٶȵĶ���v=$\frac{��x}{��t}$������t��0ʱ����ʾ������tʱ�̵�˲ʱ�ٶȣ��Dz�����ѧ�ϼ���˼�뷽����
����������ǵ�Ч����Ĺ�ϵ����̽�������������ʵ����ʹ���˵�Ч�����˼�룮
�ȱ����˶��ֳ�����С�Σ����õ�����ѧ�ϵ��ַ���
�ʵ���������������ģ������ǵ�Ч�������
��� �⣺A��٤�����о����������˶�ʱ��������������ʱ��̫�̣����ײ�������˲����ˡ��嵭�������ķ���������ʱ�䣬Ȼ���ٰѵó��Ľ��ۺ������ƣ���A��ȷ��
B���ٶȵĶ���v=$\frac{��x}{��t}$����ʾƽ���ٶȣ�����t��0ʱ����ʾ������tʱ�̵�˲ʱ�ٶȣ��Dz�����ѧ�ϼ���˼�뷽������B��ȷ��
C������ļ��ٶ��ֽ����ٶȵı仯�ʣ���ֵ�ɱ�ֵ$\frac{F}{m}$��������C����ȷ��
D�����Ƶ��ȱ����˶�λ�ƹ�ʽʱ���������˶����̻��ֳ�����С�Σ����õ�����ѧ�е�Ԫ������D��ȷ��
����ѡ����ȷ�ģ���ѡ��C��
���� ���⿼���������õ�˼ά��������ѧ�������õ�˼�뷽���м��������Ʊ���������Ч�������跨�ȵȣ�

��ϰ��ϵ�д�
�����Ŀ
17�� �ӵ����ϱ���ֲڵĽ����崦�ڵ����Ϊq�������ɵĵ糡�У����q��������ĵ糡�߷ֲ���ͼ��ʾ���������˴˾�Ե���������Ϊ+Q������Ϊm�Ļ��飬�ؽ�������ϱ����ɾ�ֹ���£��Ի����»��Ĺ��̣�����˵����ȷ���ǣ�������
�ӵ����ϱ���ֲڵĽ����崦�ڵ����Ϊq�������ɵĵ糡�У����q��������ĵ糡�߷ֲ���ͼ��ʾ���������˴˾�Ե���������Ϊ+Q������Ϊm�Ļ��飬�ؽ�������ϱ����ɾ�ֹ���£��Ի����»��Ĺ��̣�����˵����ȷ���ǣ�������
 �ӵ����ϱ���ֲڵĽ����崦�ڵ����Ϊq�������ɵĵ糡�У����q��������ĵ糡�߷ֲ���ͼ��ʾ���������˴˾�Ե���������Ϊ+Q������Ϊm�Ļ��飬�ؽ�������ϱ����ɾ�ֹ���£��Ի����»��Ĺ��̣�����˵����ȷ���ǣ�������
�ӵ����ϱ���ֲڵĽ����崦�ڵ����Ϊq�������ɵĵ糡�У����q��������ĵ糡�߷ֲ���ͼ��ʾ���������˴˾�Ե���������Ϊ+Q������Ϊm�Ļ��飬�ؽ�������ϱ����ɾ�ֹ���£��Ի����»��Ĺ��̣�����˵����ȷ���ǣ�������| A�� | ����Ļ�е���غ� | B�� | ����ļ��ٶ��ȼ�С������ | ||
| C�� | ����ĵ����ܲ��� | D�� | ���������Ĺ����ڶ��ܵı仯�� |
17�� ��ͼ��ʾ��ˮƽ���õ�ƽ�н�����������γ���ǿ�ų���������Ϊd��һ�������Һ�δ��������СΪq������Ϊm�����°��Ե����糡����ֱ�ߴ��ϰ��Ե�������֪�������ٶ�Ϊg��������˵��$\underset{��}{•}$$\underset{��}{•}$$\underset{ȷ}{•}$���ǣ�������
��ͼ��ʾ��ˮƽ���õ�ƽ�н�����������γ���ǿ�ų���������Ϊd��һ�������Һ�δ��������СΪq������Ϊm�����°��Ե����糡����ֱ�ߴ��ϰ��Ե�������֪�������ٶ�Ϊg��������˵��$\underset{��}{•}$$\underset{��}{•}$$\underset{ȷ}{•}$���ǣ�������
 ��ͼ��ʾ��ˮƽ���õ�ƽ�н�����������γ���ǿ�ų���������Ϊd��һ�������Һ�δ��������СΪq������Ϊm�����°��Ե����糡����ֱ�ߴ��ϰ��Ե�������֪�������ٶ�Ϊg��������˵��$\underset{��}{•}$$\underset{��}{•}$$\underset{ȷ}{•}$���ǣ�������
��ͼ��ʾ��ˮƽ���õ�ƽ�н�����������γ���ǿ�ų���������Ϊd��һ�������Һ�δ��������СΪq������Ϊm�����°��Ե����糡����ֱ�ߴ��ϰ��Ե�������֪�������ٶ�Ϊg��������˵��$\underset{��}{•}$$\underset{��}{•}$$\underset{ȷ}{•}$���ǣ�������| A�� | Һ������������ֱ���˶� | B�� | Һ���������ȼ���ֱ���˶� | ||
| C�� | ����ĵ��Ʋ�Ϊmg$\frac{d}{q}$ | D�� | Һ�εĵ����ܼ�����mgd |
1��������ֱ���˶�������ٶȺͼ��ٶȵĹ�ϵ������˵������ȷ���ǣ�������
| A�� | �ٶȱ仯Խ�������ٶȾ�ԽС | |
| B�� | ���ٶȷ��ֲ��䣬�ٶȷ���Ҳһ�����ֲ��� | |
| C�� | �ٶȱ仯Խ���ٶȾ�Խ�� | |
| D�� | ���ٶȴ�С���ϱ�С���ٶȴ�СҲһ�����ϱ�С |
11�� ��ͼ��A��B�ֱ��Ǽס�����С���ͬһ�ص���ͬһֱ���˶���v-tͼ����ͼ������жϣ�������
��ͼ��A��B�ֱ��Ǽס�����С���ͬһ�ص���ͬһֱ���˶���v-tͼ����ͼ������жϣ�������
 ��ͼ��A��B�ֱ��Ǽס�����С���ͬһ�ص���ͬһֱ���˶���v-tͼ����ͼ������жϣ�������
��ͼ��A��B�ֱ��Ǽס�����С���ͬһ�ص���ͬһֱ���˶���v-tͼ����ͼ������жϣ�������| A�� | AB��8sʱ���ص������� | B�� | ������t=8 sʱ�����Զ | ||
| C�� | �����˶������в������� | D�� | ������t=2 sʱ������� |
18������������ǿ�糡���жϴ�����ǣ�������
| A�� | ��ʽE=$\frac{F}{q}$Ҳ��������ǿ�糡 | |
| B�� | ����U=Ed��֪����ǿ�糡����������ĵ��Ʋ���������ľ�������� | |
| C�� | ��ǿ�糡�ij�ǿֵ���������ⷽ��ÿ��λ�����ϵĵ��Ʋ�ֵ | |
| D�� | ��ǿ�糡�ij�ǿ�������Ǹ���������ܵ糡���ķ���һ�� |
16��ƽ������ij��ٶ�ΪV0��ĩ�ٶ�Vt�������ʱ���ǣ�������
| A�� | $\frac{V_0}{g}$ | B�� | $\frac{V_t}{g}$ | C�� | $\frac{{{V_t}-{V_0}}}{g}$ | D�� | $\frac{{\sqrt{V_t^2-V_0^2}}}{g}$ |
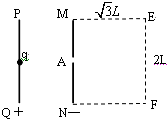 ��ͼ��ʾ��PQ��MN������������ǿ�糡��MN�����Ҳ�ij�Ϊ$\sqrt{3}$L����Ϊ2L�������������д�ֱֽ�����ǿ�ų�B������һ���ٶ�Ϊ�㡢������Ϊq������Ϊm�����ӣ�������������PQ������������糡���ٺ�MN���е�λ���ϵ�С��A��ֱ����ų�������NF�߽���ij�㴹ֱ�����߽߱��������
��ͼ��ʾ��PQ��MN������������ǿ�糡��MN�����Ҳ�ij�Ϊ$\sqrt{3}$L����Ϊ2L�������������д�ֱֽ�����ǿ�ų�B������һ���ٶ�Ϊ�㡢������Ϊq������Ϊm�����ӣ�������������PQ������������糡���ٺ�MN���е�λ���ϵ�С��A��ֱ����ų�������NF�߽���ij�㴹ֱ�����߽߱��������