��Ŀ����
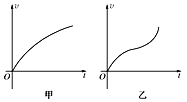
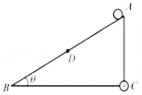
����Ŀ����ͼ��ʾ��ABCDO�Ǵ�����ֱƽ���ڵĹ⻬�����AB�ǰ뾶ΪR=10m��![]() Բ�ܹ����CDO��ֱ��Ϊ10m�İ�Բ�����AB�����CDO���ͨ�����̵�ˮƽ��������Ⱥ��Բ��ƣ�ƽ�����ӡ��뾶OA����ˮƽλ�ã�ֱ��OC������ֱλ�á�һ��С��P��A������Ϸ���H���������£���A�������ֱƽ���ڵĹ���˶���С��A��ʱ��е����ʧ������С��ͨ��CDO�����͵�Cʱ�Թ����ѹ��������������6.5����ȡgΪ10m/s2��
Բ�ܹ����CDO��ֱ��Ϊ10m�İ�Բ�����AB�����CDO���ͨ�����̵�ˮƽ��������Ⱥ��Բ��ƣ�ƽ�����ӡ��뾶OA����ˮƽλ�ã�ֱ��OC������ֱλ�á�һ��С��P��A������Ϸ���H���������£���A�������ֱƽ���ڵĹ���˶���С��A��ʱ��е����ʧ������С��ͨ��CDO�����͵�Cʱ�Թ����ѹ��������������6.5����ȡgΪ10m/s2��
(1)����߶�H�Ĵ�С��
(2)�����۴����ܷ�CDO�������ߵ�O����˵�����ɣ�
(3)��С���ع���˶����������һ����ع����ʱ���ٶȴ�С��

���𰸡�(1)3.75m��(2)�ܣ���������(3)![]()
��������
(1)��C�㣬����ţ�ٵڶ�����
![]()
![]()
![]()
��P�㵽C�㣬���ݶ��ܶ���
![]()
�������
![]()
(2)��C�㵽O�㣬���ݶ��ܶ���
![]()
�������
![]()
������ǡ�õ�����O����ٶȴ�СΪv0������ţ���˶����ɵ�
![]()
���
![]()
����
![]()
����С�����ͨ��O�㡣
(3)С���뿪O�����ƽ���˶�������ƽ���˶������У�ˮƽ����
![]()
��ֱ����
![]()
����
![]()
�������
![]()
����С���ٴ��䵽����ϵ��ٶ�
![]()
�������ݽ��
![]()

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ