题目内容
10. 质谱仪可以对气体分子进行分析.如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同价位的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达探测器.已知元电荷为e,a、b板间距为d,极板M、N的长度和间距均为L.不计离子重力及进入a板时的初速度.在a、b间加上电压U1,在M、N间加上垂直于纸面的匀强磁场,磁感应强度为B,若进入a、b间的所有离子质量均为m,要使所有的离子均能通过控制区从右侧飞出,a、b间的加速电压U1至少为多少?
质谱仪可以对气体分子进行分析.如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同价位的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达探测器.已知元电荷为e,a、b板间距为d,极板M、N的长度和间距均为L.不计离子重力及进入a板时的初速度.在a、b间加上电压U1,在M、N间加上垂直于纸面的匀强磁场,磁感应强度为B,若进入a、b间的所有离子质量均为m,要使所有的离子均能通过控制区从右侧飞出,a、b间的加速电压U1至少为多少?
分析 粒子在磁场中做的是匀速圆周运动,根据几何关系可以求得粒子的最小的半径,进而可以求得粒子的最小的速度的大小,从而可以求得在a、b间的加速电压U1
解答 解:假定n价正离子在磁场中向N板偏转,洛仑兹力充当向心力,
设轨迹半径为R,
由牛顿第二定律nevB=$\frac{m{v}^{2}}{R}$
离子刚好从N板右侧边缘穿出时,
由几何关系:R2=L2+(R-$\frac{L}{2}$)2
由以上各式得:U1=$\frac{25ne{L}^{2}{B}^{2}}{32m}$
当n=1时U1取最小值Umin=$\frac{25e{L}^{2}{B}^{2}}{32m}$
答:要使所有的离子均能通过控制区从右侧飞出,a、b间的加速电压U1至少为$\frac{25e{L}^{2}{B}^{2}}{32m}$.
点评 考查在磁场中粒子做的是匀速圆周运动,理解牛顿第二定律,及掌握几何关系的正确应用,注意求解a、b间的加速电压最小值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.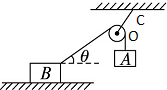 如图所示,天花板上C点,挂一轻质光滑滑轮O,两侧用细绳连着两个物体A与B,物体B放在粗糙水平地面上,A、B均静止.现将物体B向右移动一小段距离,AB仍能静止,则( )
如图所示,天花板上C点,挂一轻质光滑滑轮O,两侧用细绳连着两个物体A与B,物体B放在粗糙水平地面上,A、B均静止.现将物体B向右移动一小段距离,AB仍能静止,则( )
 如图所示,天花板上C点,挂一轻质光滑滑轮O,两侧用细绳连着两个物体A与B,物体B放在粗糙水平地面上,A、B均静止.现将物体B向右移动一小段距离,AB仍能静止,则( )
如图所示,天花板上C点,挂一轻质光滑滑轮O,两侧用细绳连着两个物体A与B,物体B放在粗糙水平地面上,A、B均静止.现将物体B向右移动一小段距离,AB仍能静止,则( )| A. | OC绳对滑轮的拉力变大,但方向不变 | |
| B. | 物体B受到地面的摩擦力变小 | |
| C. | 物体B对地面的压力可能为0 | |
| D. | 物体B对地面的压力变小 |
5. 如图所示,一倾角为30°的斜面体置于粗糙的水平面上,光滑的斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接.现对B施加一水平向左的拉力F(大小未知)使A、B均静止在斜面上,此时弹簧的长度为l,斜面体仍保持静止,重力加速度为g,则下列说法正确的是( )
如图所示,一倾角为30°的斜面体置于粗糙的水平面上,光滑的斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接.现对B施加一水平向左的拉力F(大小未知)使A、B均静止在斜面上,此时弹簧的长度为l,斜面体仍保持静止,重力加速度为g,则下列说法正确的是( )
 如图所示,一倾角为30°的斜面体置于粗糙的水平面上,光滑的斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接.现对B施加一水平向左的拉力F(大小未知)使A、B均静止在斜面上,此时弹簧的长度为l,斜面体仍保持静止,重力加速度为g,则下列说法正确的是( )
如图所示,一倾角为30°的斜面体置于粗糙的水平面上,光滑的斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接.现对B施加一水平向左的拉力F(大小未知)使A、B均静止在斜面上,此时弹簧的长度为l,斜面体仍保持静止,重力加速度为g,则下列说法正确的是( )| A. | 斜面体一定受到水平面的摩擦力作用,且方向水平向左 | |
| B. | 弹簧原长为l-$\frac{mg}{2k}$,拉力F的大小为$\frac{2\sqrt{3}}{3}$mg | |
| C. | 弹簧原长为l+$\frac{mg}{2k}$,拉力F的大小为2$\sqrt{3}$mg | |
| D. | 斜面对两小球的作用力大小为$\frac{\sqrt{21}}{3}$mg |
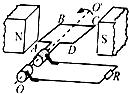 如图为交流发电机的工作原理图,线框从图示位置经过0.01s匀速转过90°时,线框与磁场方向垂直,此时线框中的感应电流最小(选填“最大”或“最小”),该发电机产生的交流电的频率为25Hz.
如图为交流发电机的工作原理图,线框从图示位置经过0.01s匀速转过90°时,线框与磁场方向垂直,此时线框中的感应电流最小(选填“最大”或“最小”),该发电机产生的交流电的频率为25Hz.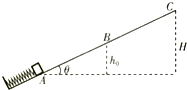 如图所示,一劲度系数很大的轻弹簧一端固定在倾角θ=30°的斜面底端,将弹簧压缩至A点锁定,然后将一质量为m的小物块紧靠弹簧放置,物块与斜面问动摩擦因数?=$\frac{\sqrt{3}}{6}$.解除弹簧锁定,物块恰能上滑至B点,A、B两点的高度差为ho,已知重力加速度为g.
如图所示,一劲度系数很大的轻弹簧一端固定在倾角θ=30°的斜面底端,将弹簧压缩至A点锁定,然后将一质量为m的小物块紧靠弹簧放置,物块与斜面问动摩擦因数?=$\frac{\sqrt{3}}{6}$.解除弹簧锁定,物块恰能上滑至B点,A、B两点的高度差为ho,已知重力加速度为g. 如图所示,在磁感应强度为B、足够大的水平匀强磁场中,有两块长为2L,间距为d的竖直放置的平行带电金属板,从CD板的正中央O点由静止释放一个初速为零的电子,电子恰好从AB板的边缘A端平行于AB板射出,且能回到O点.已知电子的电荷量为e,质量为m,重力可忽略不计,电场只局限于平行板之间,且L>d.
如图所示,在磁感应强度为B、足够大的水平匀强磁场中,有两块长为2L,间距为d的竖直放置的平行带电金属板,从CD板的正中央O点由静止释放一个初速为零的电子,电子恰好从AB板的边缘A端平行于AB板射出,且能回到O点.已知电子的电荷量为e,质量为m,重力可忽略不计,电场只局限于平行板之间,且L>d.