Question

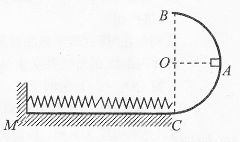
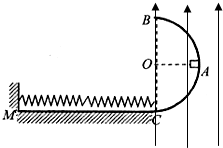如图所示，光滑半圆弧绝缘轨道半径为R，OA为水平半径，BC为竖直直径．一质量为m且始终带+q电量的小物块自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平绝缘滑道CM上，在水平滑道上有一轻弹簧，其一端固定在竖直墙上，另一端恰位于滑道的末端C点，此时弹簧处于自然状态．物块运动过程中弹簧最大弹性势能为E_P，物块被弹簧反弹后恰能通过B点．己知物块与水平滑道间的动摩擦因数为μ，直径BC右侧所处的空间（包括BC边界）有竖直向上的匀强电场，且电场力为重力的一半．求：
（1）弹簧的最大压缩量d；
（2）物块从A处开始下滑时的初速度v₀．

Answer 1

分析：（1）由题意，物块恰能通过B点，由重力和电场力的合力提供向心力，根据牛顿第二定律可求得通过B点的速度．物块由C到B过程和弹簧从压缩到最短开始，至物块被弹离弹簧的过程中，由动能定理或能量守恒定律列式求解即可．
（2）物块从A处下滑至弹簧被压缩到最短的过程中，由能量守恒定律列式求解v₀即可．

解答：解：（1）设物块刚离开弹簧时速度为v₁，恰能通过B点时的速度为v₂．
由题意可知：
   mg-qE=m

v 2 2

R

 ①
又qE=0.5mg  ②
在物块由C点运动到B点的过程中，由动能定理得：
  qE?2R-2mgR=

1

2

m

v

2 2

-

1

2

m

v

2 1

  ③
解得 v₁=

2.5gR

弹簧从压缩到最短开始，至物块被弹离弹簧的过程中，由能量守恒定律得：
 

1

2

m

v

2 1

+μmgd=E_p ④
联立③④解得：d=

Ep

μmg

-

5R

2μ

 ⑤
（2）物块从A处下滑至弹簧被压缩到最短的过程中，由能量守恒定律得：
 

1

2

m

v

2 0

+mgR=E_p+μmgd ⑥
解⑤⑥可得：v₀=

4Ep m - 9gR 2

 ⑦
答：
（1）弹簧的最大压缩量d是

Ep

μmg

-

5R

2μ

；
（2）物块从A处开始下滑时的初速度v₀是

4Ep m - 9gR 2

．

点评：本题关键要细心分析物块的运动过程和状态，找出最高点B的临界条件，抓住过程中能量守恒是解题的关键．