题目内容
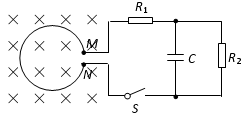
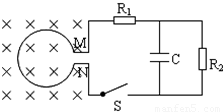
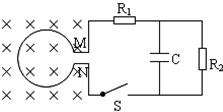 如图所示,匝数N=100匝、截面积S=0.2m2、电阻r=0.5Ω的圆形线圈MN处于垂直纸面向里的匀强磁场内,磁感应强度随时间按B=0.6+0.02t(T)的规律变化,处于磁场外的电阻R1=3.5Ω,R2=6Ω,电容C=30μF,开关S开始时未闭合,求:
如图所示,匝数N=100匝、截面积S=0.2m2、电阻r=0.5Ω的圆形线圈MN处于垂直纸面向里的匀强磁场内,磁感应强度随时间按B=0.6+0.02t(T)的规律变化,处于磁场外的电阻R1=3.5Ω,R2=6Ω,电容C=30μF,开关S开始时未闭合,求:(1)闭合S后,线圈两端M、N两点间的电压UMN和电阻R2消耗的电功率;
(2)闭合S一段时间后又打开S,则S断开后通过R2的电荷量为多少?
分析:(1)据题,磁感应强度随时间按B=0.6+0.02t(T)的规律变化,线圈中产生感应电动势,由此式得到磁感应强度的变化率为
=0.02T/s,由法拉第电磁感应定律求出感应电动势,由欧姆定律求出感应电流的大小.M、N两点间的电压UMN是外电压,由闭合电路欧姆定律求出,R2消耗的电功率:P2=I2R2.
(2)闭合S一段时间后电容器充电,电容器的电压为UC=IR2,电量Q=CUC,S断开后通过R2的电荷量等于电容器所带电荷量.
| △B |
| △t |
(2)闭合S一段时间后电容器充电,电容器的电压为UC=IR2,电量Q=CUC,S断开后通过R2的电荷量等于电容器所带电荷量.
解答:解:(1)由题给条件可知磁感应强度的变化率为:
=0.02T/s
故回路产生的电动势为:E=N
=N
s=0.4v
感应电流:I=
=0.04A
由闭合电路欧姆定律有:UMN=E-Ir=0.38V
故R2消耗的电功率:P2=I2R2=9.6×10-3W
(2)S合时:UC=IR2=0.24V
充电电量:Q=CUC=7.2×10-6C
S开时:R2放电,放电的电量:Q=7.2×10-6C,即为S断开后通过R2的电荷量.
答:
(1)闭合S后,线圈两端M、N两点间的电压UMN是0.38V,电阻R2消耗的电功率是9.6×10-3W;
(2)闭合S一段时间后又打开S,则S断开后通过R2的电荷量为7.2×10-6C.
| △B |
| △t |
故回路产生的电动势为:E=N
| △φ |
| △t |
| △B |
| △t |
感应电流:I=
| E |
| R1+R2+r |
由闭合电路欧姆定律有:UMN=E-Ir=0.38V
故R2消耗的电功率:P2=I2R2=9.6×10-3W
(2)S合时:UC=IR2=0.24V
充电电量:Q=CUC=7.2×10-6C
S开时:R2放电,放电的电量:Q=7.2×10-6C,即为S断开后通过R2的电荷量.
答:
(1)闭合S后,线圈两端M、N两点间的电压UMN是0.38V,电阻R2消耗的电功率是9.6×10-3W;
(2)闭合S一段时间后又打开S,则S断开后通过R2的电荷量为7.2×10-6C.
点评:本题电磁感应与电路知识的综合应用,关键是求解感应电动势.

练习册系列答案
相关题目
 如图所示,匝数为100匝、面积为0.01m2的线圈,处于磁感应强度B1为
如图所示,匝数为100匝、面积为0.01m2的线圈,处于磁感应强度B1为 如图所示,匝数为100、面积为0.01m2的线圈,处于磁感应强度B1为
如图所示,匝数为100、面积为0.01m2的线圈,处于磁感应强度B1为