题目内容
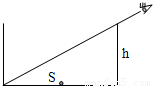
如图所示,有一个圆桶形容器的底面直径d=
m,桶高h=1m,桶底的圆心S点有一小突起.当桶内不装液体时,人从右边某位置沿桶的上边缘向下看去,刚好能看到桶底的最左端.现在缓慢地向桶内倒入折射率为n=
的某种透明液体:
(1)液面上升的高度x等于多少时,人在原位置刚好能看到桶底圆心处的小突起S?
(2)若光在真空中的传播速度c=3.0×108m/s,求光在这种液体中的传播速度v.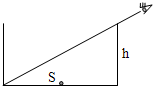
| 3 |
| 3 |
(1)液面上升的高度x等于多少时,人在原位置刚好能看到桶底圆心处的小突起S?
(2)若光在真空中的传播速度c=3.0×108m/s,求光在这种液体中的传播速度v.

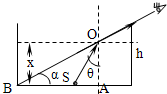
(1)光路图如图所示,由题意,tanα=
| h |
| d |
| ||
| 3 |
由折射率公式:n=
| sin(90°-α) |
| sinθ |
得:sinθ=
| sin(90°-30°) |
| n |
解得:θ=30°
由几何关系有:SO=SB=
| d |
| 2 |
| ||
| 2 |
则:x=SO?cosθ=
| ||
| 2 |
| ||
| 2 |
(2)由n=
| c |
| v |
v=
| c |
| n |
| 3 |
答:(1)液面上升的高度x等于0.75m时,人在原位置刚好能看到桶底圆心处的小突起S.
(2)光在这种液体中的传播速度
| 3 |

练习册系列答案
相关题目
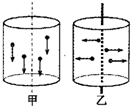 为模拟净化空气过程,有人设计了如图所示的含有灰尘空气的密闭玻璃圆柱桶(圆桶的高和直径相等).第一种除尘方式是:在圆柱桶顶面和底面间加上电压U,沿圆柱桶的轴线方向形成一个匀强电场,尘粒运动方向如图甲所示;第二种除尘方式是:圆柱桶轴线处放一直导线,在导线与容器壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即f=kv(k为一定值),假设每个尘粒的质量和电量均相同,重力可忽略不计,则在这两种方式中( )
为模拟净化空气过程,有人设计了如图所示的含有灰尘空气的密闭玻璃圆柱桶(圆桶的高和直径相等).第一种除尘方式是:在圆柱桶顶面和底面间加上电压U,沿圆柱桶的轴线方向形成一个匀强电场,尘粒运动方向如图甲所示;第二种除尘方式是:圆柱桶轴线处放一直导线,在导线与容器壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即f=kv(k为一定值),假设每个尘粒的质量和电量均相同,重力可忽略不计,则在这两种方式中( )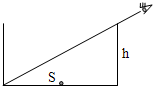 如图所示,有一个圆桶形容器的底面直径d=
如图所示,有一个圆桶形容器的底面直径d=
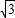 m,桶高h=1m,桶底的圆心S点有一小突起.当桶内不装液体时,人从右边某位置沿桶的上边缘向下看去,刚好能看到桶底的最左端.现在缓慢地向桶内倒入折射率为n=
m,桶高h=1m,桶底的圆心S点有一小突起.当桶内不装液体时,人从右边某位置沿桶的上边缘向下看去,刚好能看到桶底的最左端.现在缓慢地向桶内倒入折射率为n=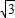 的某种透明液体:
的某种透明液体: