Question

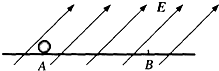如图所示，带正电小球质量为m=1×10^-2kg，带电量为q=l×10^-6C，置于光滑绝缘水平面上的A点．当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得其速度v_B=1.5m/s，此时小球的位移为S=0.15m．求此匀强电场场强E的取值范围．（g=10m/s．） 
某同学求解如下：设电场方向与水平面之间夹角为θ，由动能定理qEScosθ=

1

2

m

v

2 B

-0得E=

m v 2 B

2qScosθ

=

75000

cosθ

V/m．由题意可知θ＞0，所以当E＞7.5×10⁴V/m时小球将始终沿水平面做匀加速直线运动．经检查，计算无误．该同学所得结论是否有不完善之处？若有请予以补充．

Answer 1

分析：由题意可知粒子受斜向上的电场力，沿水平方向分力使物体做加速运动，沿竖直向上的分力与重力和支持力平衡，则应考虑小球是否会离开水平面．

解答：解：该同学所得结论有不完善之处．
为使小球始终沿水平面运动，电场力在竖直方向的分力必须小于等于重力，即：qEsinθ≤mg
所以sinθ≤

mg

Eq

；
因Eq=

m v 2 B

2Scosθ

tanθ≤

2mgS

m v 2 B

=

2Sg

v 2 B

=

4

3

故E≤

mg

qsinθ

=

1×10-2×10

1×10-6× 4 5

V/m=1.25×105V/m
即：7.5×10⁴V/m＜E≤1.25×10⁵V/m

点评：本题中不但要考虑物体在水平面上的运动，还应考虑物体是否会离开水平面，故应有最大值存在．