题目内容
【题目】在一次警车A追击劫匪车B时,两车同时由静止向同一方向加速行驶,经过30 s追上。两车各自的加速度为aA=12 m/s2,aB=8 m/s2,各车最高时速分别为vA=48 m/s,vB=40 m/s,问追上时两车各行驶多少路程?原来相距多远?
【答案】1344m;1 100 m;244 m
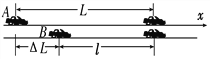
【解析】如图所示,以A车的初始位置为坐标原点,Ax为正方向,设L为警车追上劫匪车所走过的全程,l为劫匪车走过的全程。则两车原来的间距为ΔL=L-l
![]()
设两车加速运动用的时间分别为tA1、tB1,
以最大速度匀速运动的时间分别为tA1、tB2,
则vA=aA tA1,解得tA1=4 s则tA2=26 s
同理tB1=5 s,tB2=25 s
警车在0~3 s时间段内做匀加速运动,L1=![]() aA tA12
aA tA12
在3~30 s时间段内做匀速运动,则L2=vA tA2
警车追上劫匪车的全部行程为L=L1+L2=![]() aA tA12+vA tA2=1344 m
aA tA12+vA tA2=1344 m
同理劫匪车被追上时的全部行程为l=l1+l2=![]() aB tB12+vB tB2=1 100m
aB tB12+vB tB2=1 100m
两车原来相距ΔL=L-l=244m

练习册系列答案
相关题目