题目内容
【题目】空间有一圆柱形匀强磁场区域，O点为圆心．磁场方向垂直于纸面向外．一带正电的粒子从A点沿图示箭头方向以速率v射入磁场，θ=30°，粒子在纸面内运动，经过时间t离开磁场时速度方向与半径OA垂直．不计粒子重力．若粒子速率变为 
，其它条件不变，粒子在圆柱形磁场中运动的时间为（ ）
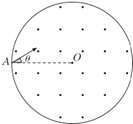
A.
B.t
C.
D.2t
【答案】C
【解析】解：设粒子电量为q，质量为m，磁场半径为r，运动的轨迹半径分别为R，磁感应强度为B，
根据洛伦兹力提供向心力：qvB=m 
①
粒子运动周期：T= 
②
联立可得：T= 
可知速度变化前后，两次粒子的周期不变，
设以速率v射入磁场时运动轨迹的半径为R1 ， 圆心为O1 ， 画出粒子运动过程图如图一所示，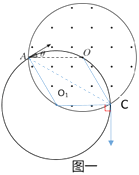
根据题意可知：AO∥O1C，AO=OC，AO1=O1C
可得：∠OAC=∠ACO1=∠CAO1=∠OCA=30°
所以可知四边形OAO1C为菱形，粒子在磁场中运动所转过的圆心角：θ1=∠AO1C=120°，
半径R1=r ③
设以速率v射入磁场时运动轨迹的半径为R2 ， 圆心为O2 ，
根据①③式可知当粒子的速度变为 
时，粒子半径R2= 
，根据几何关系画出粒子运动过程图如图二所示，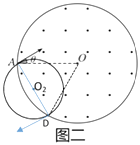
粒子所转过的圆心角θ2=180°
根据粒子在磁场中运动的时间：t′= 
T
所以两次粒子在磁场中运动的时间之比： 
= 
= 
= 
又因为t1=t，所以t2= 
故C正确，ABD错误
故选：C．
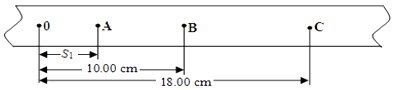
【题目】在做“研究匀变速直线运动”的实验时，某同学得到一条用电火花计时器打下的纸带如图1所示，并在其上取了A、B、C、D、E、F、G 7个计数点，每相邻两个计数点间还有4个点图中没有画出，电火花计时器接频率为f的交流电源．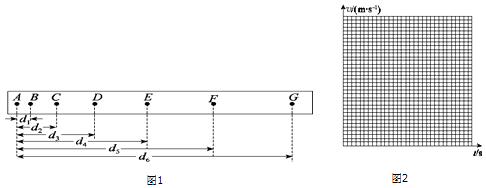
（1）计算F点的瞬时速度VF的公式为VF= ，
用“逐差法”计算加速度的公式a= ． （用dn和f表示）；
（2）他经过测量并计算得出电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表．以A点对应的时刻为t=0，试在如图所示坐标系中合理地选择标度，在图2中作出vt图象 ， 并利用该图象求出物体的加速度am/s2；（保留两位有效数字）
对应点 | B | C | D | E | F |
速度（m/s） | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
（3）如果当时电网中交变电流的电压偏低，而做实验的同学并不知道，那么加速度的测量值与实际值相比 ． （填“偏大”、“偏小”或“不变”）
