题目内容
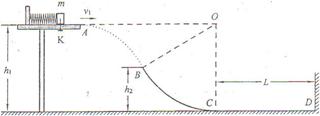
(14分) 如图所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷量,质量分别为mA和mB.两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与B连接,另一端连接一轻质小钩.整个装置处于场强为E、方向水平向左的匀强电场中. A、B开始时静止,已知弹簧的劲度系数为k,不计一切摩擦及A、B间的库仑力,A、B所带电荷量保持不变,B不会碰到滑轮.
(1) 若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力恰为零,但不会离开P,求物块C下降的最大距离;
(2) 若C的质量改为2M,则当A刚离开挡板P时,B的速度多大?
(1)h=E(QB+QA)/k (2)V=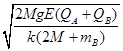
解析试题分析:(1)开始时弹簧形变量为x1,由平衡条件:
Kx1=EQB 可得x1="EQ/k"
设当A刚离开档板时弹簧的形变量为x2:
由:kx2=EQA 可得x2=EQA/k
故C下降的最大距离为:h=x1+x2
解得h=E(QB+QA)/k
(2)由能量守恒定律可知:C下落h过程中,C重力势能的减少量等于B的电势能的增量和弹簧弹性势能的增量以及系统动能的增量之和
当C的质量为M时:Mgh=QBEh+ΔE弹
当C的质量为2M时,设A刚离开挡板时B的速度为V
2Mgh=QBEh+ΔE弹+(2M+mB)V2/2
解得A刚离开P时B的速度为:V=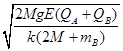
考点:本题考查对胡克定律、能量守恒定律的应用。

地面上方某一高度有一小球,其重力势能为10J,现让它由静止开始下落,若不计空气阻力,则它在着地前瞬间的动能为( )
| A.10 J | B.30 J | C.5J | D.20J |
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体 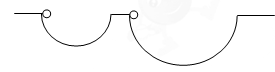
| A.机械能均逐渐减小 |
| B.经最低点时动能相等 |
| C.在最低点对轨道的压力相等 |
| D.在最低点的机械能不相等 |
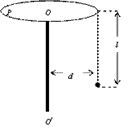
如图所示,在小车的支架上用细线悬挂一个小球,已知线长为L,小车带着小球一起以速度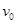 向右做匀速运动。当小车突然碰到障碍物而停止运动后,关于小球再上升的最大高度h的下列几种表述中,肯定不可能的是( )
向右做匀速运动。当小车突然碰到障碍物而停止运动后,关于小球再上升的最大高度h的下列几种表述中,肯定不可能的是( )
A.小于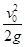 | B.大于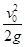 | C.等于 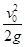 | D.等于2L |
光滑斜面上物块A被平行斜面的轻质弹簧拉住静止于O点,如图所示,现将A沿斜面拉到B点无初速释放,物体在BC范围内做简谐运动,则下列说法正确的是: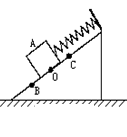
| A.OB越长,振动能量越大 |
| B.在振动过程中,物体A机械能守恒 |
| C.A在C点时,物体与弹簧构成的系统势能最大,在O点时系统势能最小 |
| D.B点时物体A的机械能最小 |

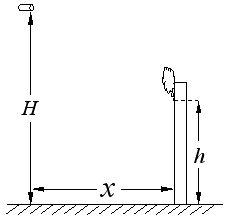
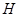 ,建筑物上的火点离地高度为
,建筑物上的火点离地高度为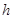 ,水炮与火点的水平距离为
,水炮与火点的水平距离为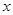 ,水泵的功率为
,水泵的功率为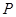 ,整个供水系统的效率
,整个供水系统的效率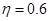 .假设水从水炮水平射出,不计空气阻力,取
.假设水从水炮水平射出,不计空气阻力,取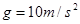 .
.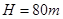 ,
,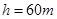 ,水炮出水速度
,水炮出水速度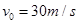 ,求水炮与起火建筑物之间的水平距离
,求水炮与起火建筑物之间的水平距离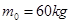 ,求水泵的功率
,求水泵的功率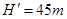 ,假设供水系统的效率
,假设供水系统的效率 不变,水炮出水口的横截面积不变,水泵功率应调整为
不变,水炮出水口的横截面积不变,水泵功率应调整为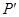 ,则
,则